题目内容
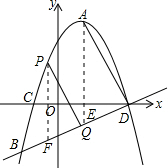
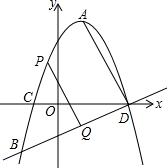 如图,抛物线的顶点坐标是A(1,4),且经过点B(-
如图,抛物线的顶点坐标是A(1,4),且经过点B(- ,-
,- ),与横轴交于C,D两点(点C在点D的左边)
),与横轴交于C,D两点(点C在点D的左边)
(1)求抛物线的解析式;
(2)连接AD,判断AD与BD的位置关系,并说明理由;
(3)设点P是直线BD上方且位于抛物线上的一动点,过点P作PQ∥AD交直线BD于点Q,求PQ的最大值.
解:(1)设抛物线解析式为y=a(x-1)2+4,
将点B的坐标代入可得:- =a(-
=a(- -1)2+4,
-1)2+4,
解得:a=-1,
故抛物线解析式为:y=-(x-1)2+4=-x2+2x+3;
(2)令y=0,则-x2+2x+3=0,
解得:x1=-1,x2=3,
∴C的坐标为(-1,0),D的坐标为(3,0),
则AD=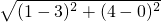 =2
=2 ,BD=
,BD=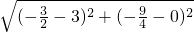 =
=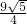 ,AB=
,AB=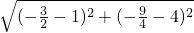 =
=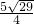 ,
,
∵AD2+BD2=AB2,
∴△ABD是直角三角形,
∴AD⊥BD;
(3)设直线BD的解析式为y=kx+b,
将B、D的坐标代入可得: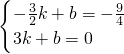 ,
,
解得: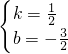 ,
,
则直线BD的解析式为y= x-
x- ,
,
过点A作AE∥y轴,交BD于点E,作PF∥y轴,交BD于点F,
则点E的坐标为(1,-1),AE=5,cos∠EAD= =
= ,
,
设点P的坐标为(x,-x2+2x+3),则点F的坐标为(x, x-
x- ),PF=-x2+2x+3-(
),PF=-x2+2x+3-( x-
x- )=-x2+
)=-x2+ x+
x+ ,
,
在Rt△PFQ中,PQ=PFcos∠FPQ=PFcos∠EAD
= (-x2+
(-x2+ x+
x+ )
)
=- (2x2-3x-9)
(2x2-3x-9)
=- (2x2-3x)+
(2x2-3x)+
=- (x-
(x- )2+
)2+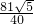 ,
,
当x= 时,PQ取得最大,最大值为
时,PQ取得最大,最大值为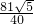 .
.
分析:(1)设抛物线解析式为y=a(x-1)2+4,将点B的坐标代入可得a的值,继而可确定抛物线的解析式;
(2)分别求出AB、BD、AD的长度,利用勾股定理的逆定理可判断AD⊥BD;
(3)过点A作AE∥y轴,交BD于点E,作PF∥y轴,交BD于点F,先求出cos∠EAD,设点P的坐标为(x,-x2+2x+3),表示出PF,继而在Rt△PQF中,可表示出PQ,利用配方法求解最值即可.
点评:本题考查了二次函数的综合,涉及了待定系数法求抛物线解析式、勾股定理的逆定理及配方法求二次函数的最值,综合考察的知识点较多,解答本题注意数形结合思想的运算.
将点B的坐标代入可得:-
 =a(-
=a(- -1)2+4,
-1)2+4,解得:a=-1,
故抛物线解析式为:y=-(x-1)2+4=-x2+2x+3;
(2)令y=0,则-x2+2x+3=0,
解得:x1=-1,x2=3,
∴C的坐标为(-1,0),D的坐标为(3,0),
则AD=
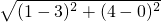 =2
=2 ,BD=
,BD=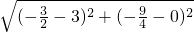 =
=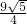 ,AB=
,AB=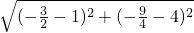 =
=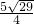 ,
,∵AD2+BD2=AB2,
∴△ABD是直角三角形,
∴AD⊥BD;
(3)设直线BD的解析式为y=kx+b,
将B、D的坐标代入可得:
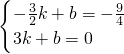 ,
,解得:
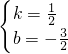 ,
,则直线BD的解析式为y=
 x-
x- ,
,过点A作AE∥y轴,交BD于点E,作PF∥y轴,交BD于点F,

则点E的坐标为(1,-1),AE=5,cos∠EAD=
 =
= ,
,设点P的坐标为(x,-x2+2x+3),则点F的坐标为(x,
 x-
x- ),PF=-x2+2x+3-(
),PF=-x2+2x+3-( x-
x- )=-x2+
)=-x2+ x+
x+ ,
,在Rt△PFQ中,PQ=PFcos∠FPQ=PFcos∠EAD
=
 (-x2+
(-x2+ x+
x+ )
)=-
 (2x2-3x-9)
(2x2-3x-9)=-
 (2x2-3x)+
(2x2-3x)+
=-
 (x-
(x- )2+
)2+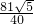 ,
,当x=
 时,PQ取得最大,最大值为
时,PQ取得最大,最大值为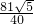 .
.分析:(1)设抛物线解析式为y=a(x-1)2+4,将点B的坐标代入可得a的值,继而可确定抛物线的解析式;
(2)分别求出AB、BD、AD的长度,利用勾股定理的逆定理可判断AD⊥BD;
(3)过点A作AE∥y轴,交BD于点E,作PF∥y轴,交BD于点F,先求出cos∠EAD,设点P的坐标为(x,-x2+2x+3),表示出PF,继而在Rt△PQF中,可表示出PQ,利用配方法求解最值即可.
点评:本题考查了二次函数的综合,涉及了待定系数法求抛物线解析式、勾股定理的逆定理及配方法求二次函数的最值,综合考察的知识点较多,解答本题注意数形结合思想的运算.

练习册系列答案
相关题目
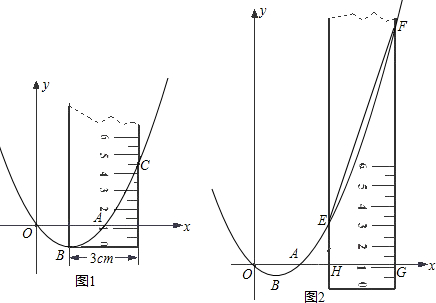
 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为 cm的等腰直角三角板ABC如图放置,BC边与x轴重合,∠ACB=90°,直角顶点C的坐标为(-3,0).
cm的等腰直角三角板ABC如图放置,BC边与x轴重合,∠ACB=90°,直角顶点C的坐标为(-3,0).
