题目内容
【题目】在![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 上运动,连接
上运动,连接![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
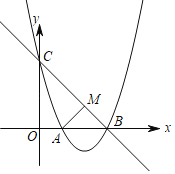
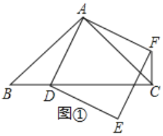
(1)如果![]() ,如图①,试判断线段
,如图①,试判断线段![]() 与
与![]() 之间的位置关系,并证明你的结论;
之间的位置关系,并证明你的结论;
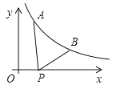
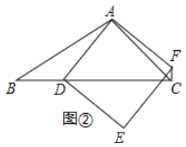
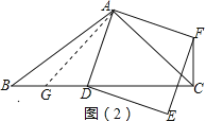
(2)如果![]() ,如图②,(1)中结论是否成立,说明理由.
,如图②,(1)中结论是否成立,说明理由.
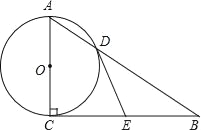
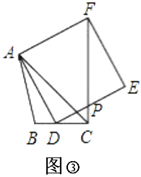
(3)如果![]() ,如图③,且正方形
,如图③,且正方形![]() 的边
的边![]() 与线段
与线段![]() 交于点
交于点![]() ,设
,设![]() ,
,![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 的长.(用含
的长.(用含![]() 的式子表示)
的式子表示)
【答案】(1)![]() ;证明见解析; (2)成立;理由见解析;(3)
;证明见解析; (2)成立;理由见解析;(3)![]() .
.
【解析】
(1)先证明![]() ,得到
,得到![]() ,再根据角度转换得到∠BCF=90°即可;
,再根据角度转换得到∠BCF=90°即可;
(2)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,可得
,可得![]() ,再证明
,再证明![]() ,得
,得![]() ,即可证明
,即可证明![]() ;
;
(3)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,可求出
,可求出![]() ,则
,则![]() ,根据
,根据![]() 得出相似比,即可表示出CP.
得出相似比,即可表示出CP.
(1)![]() ;
;
证明:∵![]() ,
,![]() ,
,
∴![]() ,
,
由正方形![]() 得
得![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
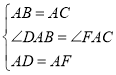 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ;
;
(2)![]() 时,
时,![]() 的结论成立;
的结论成立;
证明:如图2,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
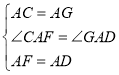 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
即![]() ;
;
(3)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
∵![]() ,
,![]()
∴△AQC为等腰直角三角形,
∵![]() ,
,
∴![]() ,
,
∵DC=x,
∴![]() ,
,
∵四边形ADEF为正方形,
∴∠ADE=90°,
∴∠PDC+∠ADQ=90°,
∵∠ADQ+∠QAD=90°,
∴∠PDC=∠QAD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目