题目内容
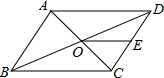 如图,?ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为16cm,则△DOE的周长是________cm.
如图,?ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为16cm,则△DOE的周长是________cm.
8
分析:根据平行四边形的对边相等和对角线互相平分可得,BC=AD,DC=AB,DO=BO,E点是CD的中点,可得OE是△DCB的中位线,可得OE= BC.从而得到结果是8cm.
BC.从而得到结果是8cm.
解答:∵四边形ABCD是平行四边形,
∴O是BD中点,△ABD≌△CDB,
又∵E是CD中点,
∴OE是△BCD的中位线,
∴OE= BC,
BC,
即△DOE的周长= △BCD的周长,
△BCD的周长,
∴△DOE的周长= △DAB的周长.
△DAB的周长.
∴△DOE的周长= ×16=8cm.
×16=8cm.
故答案为:8.
点评:本题主要考查平行四边形的性质及三角形中位线的性质的应用.
分析:根据平行四边形的对边相等和对角线互相平分可得,BC=AD,DC=AB,DO=BO,E点是CD的中点,可得OE是△DCB的中位线,可得OE=
 BC.从而得到结果是8cm.
BC.从而得到结果是8cm.解答:∵四边形ABCD是平行四边形,
∴O是BD中点,△ABD≌△CDB,
又∵E是CD中点,
∴OE是△BCD的中位线,
∴OE=
 BC,
BC,即△DOE的周长=
 △BCD的周长,
△BCD的周长,∴△DOE的周长=
 △DAB的周长.
△DAB的周长.∴△DOE的周长=
 ×16=8cm.
×16=8cm.故答案为:8.
点评:本题主要考查平行四边形的性质及三角形中位线的性质的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 如图,?ABCD的两条对角线AC、BD相交于点O,问图中全等的三角形有哪几对?
如图,?ABCD的两条对角线AC、BD相交于点O,问图中全等的三角形有哪几对? 如图,?ABCD的两条对角线AC、BD相交于点O,那么,图中有几对三角形全等( )
如图,?ABCD的两条对角线AC、BD相交于点O,那么,图中有几对三角形全等( ) 如图,?ABCD的两条对角线AC,BD相交于点O,则图中全等的三角形有( )对.
如图,?ABCD的两条对角线AC,BD相交于点O,则图中全等的三角形有( )对.