题目内容
 已知抛物线y=
已知抛物线y=| 1 | 4 |
(1)当动点P在该抛物线上运动时,求证:P到定直线l的距离PP′等于P到定点F的距离.
(2)若过定点F任作一条直线,与抛物线交于M、N两点,再以线段MN的长为直径作一个圆C,试判断圆C与定直线l的位置关系,并说明理由.
(3)在(2)的条件下,你能否在定直线l上找到一点Q,使得QF恰好平分∠MQN?若能,求出点坐标;否则,说明理由.
分析:(1)根据抛物线解析式设出点P的坐标为(x,
x2),根据勾股定理表示求出PF,再根据点到直线的距离表示出点P到直线l的距离,即可得证;
(2)过M、N、C分别作直线l的垂线,垂足分别为E、G、H,可得CH是梯形MEGN的中位线,根据梯形的中位线定理可得CH=
(ME+NG),再根据(1)的结论代入整理可得CH=
MN,再根据直线与圆的位置关系可以判断圆C与定直线l相切;
(3)根据角平分线的性质可得
=
,再根据ME=MF,NG=NF,可以判断Rt△MEQ和Rt△NGQ相似,根据相似三角形对应角相等可得∠MQE=∠NQG,又因为QF平分∠MQN,推出∠EQF=90°,从而得到点Q在y轴上,即Q为定值线与y轴的交点.
| 1 |
| 4 |
(2)过M、N、C分别作直线l的垂线,垂足分别为E、G、H,可得CH是梯形MEGN的中位线,根据梯形的中位线定理可得CH=
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据角平分线的性质可得
| MF |
| NF |
| MQ |
| NQ |
解答:(1)证明:∵点P在抛物线y=
x2上,
∴设点P(x,
x2),
则PF=
=
=
x2+1,
∵定直线l的方程为:y=-1,
∴点P到直线l的距离PP′=
x2-(-1)=
x2+1,
∴P到定直线l的距离PP′等于P到定点F的距离;
(2)解:圆C与定直线l的位置关系是相切.理由如下:
如图,过M、N、C分别作直线l的垂线,垂足分别为E、G、H,
则CH是梯形MEGN的中位线,
∵ME=MF,NG=NF,
∴CH=
(ME+NG)=
(MF+NF)=
MN,
即圆心C到定直线l的距离等于⊙C的半径,
∴圆C与定直线l的位置关系是相切;
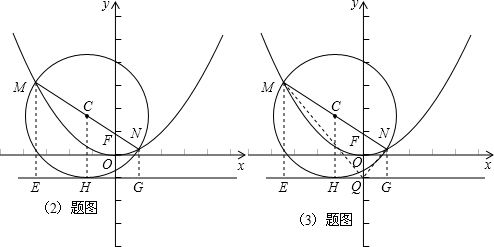
(3)解:存在点Q(0,-1),使得QF恰好平分∠MQN.
理由如下:∵QF平分∠MQN,
∴
=
,
∵ME=MF,NG=NF,
∴
=
,
∴Rt△MEQ∽Rt△NGQ,
∴∠MQE=∠NQG,
又∵QF平分∠MQN,
∴∠MQF=∠NQF,
∵∠MQE+∠MQF+∠NQF+∠NQG=180°,
∴∠MQE+∠MQF=
×180°=90°,
∴∠EQF=90°,
∴点Q在y轴上,
即点Q为定直线l:y=-1与y轴的交点,
∴点Q的坐标为(0,-1).
| 1 |
| 4 |
∴设点P(x,
| 1 |
| 4 |
则PF=
x2+(
|
|
| 1 |
| 4 |
∵定直线l的方程为:y=-1,
∴点P到直线l的距离PP′=
| 1 |
| 4 |
| 1 |
| 4 |
∴P到定直线l的距离PP′等于P到定点F的距离;
(2)解:圆C与定直线l的位置关系是相切.理由如下:
如图,过M、N、C分别作直线l的垂线,垂足分别为E、G、H,
则CH是梯形MEGN的中位线,
∵ME=MF,NG=NF,
∴CH=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即圆心C到定直线l的距离等于⊙C的半径,
∴圆C与定直线l的位置关系是相切;

(3)解:存在点Q(0,-1),使得QF恰好平分∠MQN.
理由如下:∵QF平分∠MQN,
∴
| MF |
| NF |
| MQ |
| NQ |
∵ME=MF,NG=NF,
∴
| ME |
| NG |
| MQ |
| NQ |
∴Rt△MEQ∽Rt△NGQ,
∴∠MQE=∠NQG,
又∵QF平分∠MQN,
∴∠MQF=∠NQF,
∵∠MQE+∠MQF+∠NQF+∠NQG=180°,
∴∠MQE+∠MQF=
| 1 |
| 2 |
∴∠EQF=90°,
∴点Q在y轴上,
即点Q为定直线l:y=-1与y轴的交点,
∴点Q的坐标为(0,-1).
点评:本题综合考查了二次函数,主要利用了抛物线上点的特征,梯形的中位线定理,直线与圆的位置关系以及直角三角形相似的判断与相似三角形对应角相等的性质,(3)中角平分线的性质,三角形的角平分线分对边所成的两条线段的比等于三角形两邻边的比同学们比较生疏,要特别注意.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
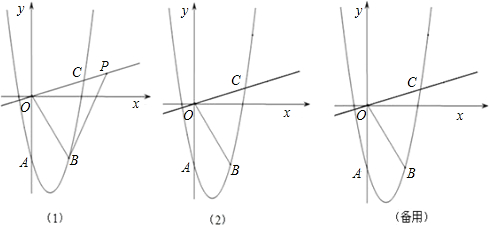
 已知抛物线y=ax2+bx+c与x轴交于A、B两点(点B在点A的右侧,且AB=8),与y轴交于点C,其中点A在x轴的负半轴上,点C在y轴的正半轴上,线段OA、OC的长(OA<OC)是方程x2-14x+48=0的两个根.
已知抛物线y=ax2+bx+c与x轴交于A、B两点(点B在点A的右侧,且AB=8),与y轴交于点C,其中点A在x轴的负半轴上,点C在y轴的正半轴上,线段OA、OC的长(OA<OC)是方程x2-14x+48=0的两个根. 已知抛物线y=ax2+bx+c与x轴交于A、B两点(点B在点A的右侧,且AB=8),与y轴交于点C,其中点A在x轴的负半轴上,点C在y轴的正半轴上,线段OA、OC的长(OA<OC)是方程x2-14x+48=0的两个根.
已知抛物线y=ax2+bx+c与x轴交于A、B两点(点B在点A的右侧,且AB=8),与y轴交于点C,其中点A在x轴的负半轴上,点C在y轴的正半轴上,线段OA、OC的长(OA<OC)是方程x2-14x+48=0的两个根.