题目内容
图中的小方格都是边长为1的正方形,△ABC的顶点和O点都在正方形的顶点上.(1)以点O为位似中心,在方格图中将△ABC放大为原来的2倍,得到△A′B′C′;
(2)△A′B′C′绕点B′顺时针旋转90°,画出旋转后得到的△A″B′C″,并求边A′B′在旋转过程中扫过的图形面积.

【答案】分析:(1)连接AO、BO、CO并延长到2AO、2BO、2CO长度找到各点的对应点,顺次连接即可.
(2)△A′B′C′的A′、C′绕点B′顺时针旋转90°得到对应点,顺次连接即可.A′B′在旋转过程中扫过的图形面积是一个扇形,根据扇形的面积公式计算即可.
解答: 解:(1)见图中△A′B′C′(4分)
解:(1)见图中△A′B′C′(4分)
(直接画出图形,不画辅助线不扣分)
(2)见图中△A″B′C″(8分)
(直接画出图形,不画辅助线不扣分)
S= π(22+42)=
π(22+42)= π•20=5π(平方单位).(10分)
π•20=5π(平方单位).(10分)
点评:本题主要考查了位似图形及旋转变换作图的方法及扇形的面积公式.
(2)△A′B′C′的A′、C′绕点B′顺时针旋转90°得到对应点,顺次连接即可.A′B′在旋转过程中扫过的图形面积是一个扇形,根据扇形的面积公式计算即可.
解答:
 解:(1)见图中△A′B′C′(4分)
解:(1)见图中△A′B′C′(4分)(直接画出图形,不画辅助线不扣分)
(2)见图中△A″B′C″(8分)
(直接画出图形,不画辅助线不扣分)
S=
 π(22+42)=
π(22+42)= π•20=5π(平方单位).(10分)
π•20=5π(平方单位).(10分)点评:本题主要考查了位似图形及旋转变换作图的方法及扇形的面积公式.

练习册系列答案
相关题目
 18、如图,图中的小方格都是边长为1的正方形,△ABC与△A/B/C/是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
18、如图,图中的小方格都是边长为1的正方形,△ABC与△A/B/C/是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上. 21、如图,图中的小方格都是边长为1的正方形,点E、A、B、C都在小正方形的顶点上.
21、如图,图中的小方格都是边长为1的正方形,点E、A、B、C都在小正方形的顶点上. 21、如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A (0,-2)、B (3,-1)、C (2,1).
21、如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A (0,-2)、B (3,-1)、C (2,1).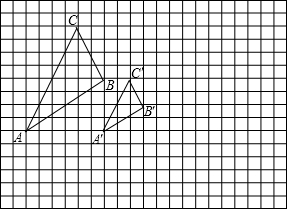 们的顶点都在小正方形的顶点上.
们的顶点都在小正方形的顶点上. 如图图中的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上,请完成以下题目
如图图中的小方格都是边长为1的正方形,△ABC的顶点都在小正方形的顶点上,请完成以下题目