题目内容
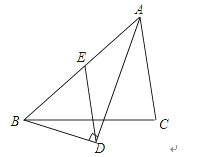
【题目】
如图，四边形
点的坐标分别为
、
、
、
，四边形关于
轴作轴对称变换得到四边形
，则
点的对应坐标为________．
四边形绕点
顺时针旋转
得到四边形
，则点的对应坐标为________．
在图中画出四边形和四边形，直接写出它们重叠部分的周长为________．
【答案】
；
；（3）
．
【解析】
(1)关于x轴作轴对称变换，点的坐标变化是：横坐标不变，纵坐标变为相反数；
(2)画出图形，直接写出点A的对应点M的坐标；
(3)根据勾股定理求出EH、MQ的长，便可求出重叠部分的周长.
解：(1)四边形EFGH如图所示，点A的对应点E的坐标为(2,-2);
(2)四边形MNPQ如图所示，点A的对应点M的坐标为(3,-1)；
(3)由勾股定理：MQ=EH=
=
重叠部分的周长=MN+FE+EH+MQ
=1+1++
=2+2
故答案为：(1)
；；（3）．
练习册系列答案
名校课堂系列答案
相关题目
