题目内容
根据题意填空：
已知，如图，AD∥BC，∠BAD=∠BCD，求证：AB∥CD．
证明：∵AD∥BC（已知）
∴∠1=( )
又∵∠BAD=∠BCD （ 已知 ）
∴∠BAD﹣∠1=∠BCD﹣∠2( )
即：∠3=∠4
∴( )．
已知，如图，AD∥BC，∠BAD=∠BCD，求证：AB∥CD．
证明：∵AD∥BC（已知）
∴∠1=( )
又∵∠BAD=∠BCD （ 已知 ）
∴∠BAD﹣∠1=∠BCD﹣∠2( )
即：∠3=∠4
∴( )．
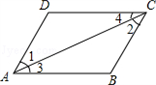
证明：
∵AD∥BC（已知）
∴∠1=∠2（两直线平行，内错角相等），
又∵∠BAD=∠BCD（已知）
∴∠BAD﹣∠1=∠BCD﹣∠2（等式性质），
即∠3=∠4，
∴AB∥CD（内错角相等，两直线平行）．
∵AD∥BC（已知）
∴∠1=∠2（两直线平行，内错角相等），
又∵∠BAD=∠BCD（已知）
∴∠BAD﹣∠1=∠BCD﹣∠2（等式性质），
即∠3=∠4，
∴AB∥CD（内错角相等，两直线平行）．
练习册系列答案
相关题目
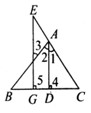20、根据题意结合图形填空：已知：如图，AD⊥BC于D，EG⊥BC与G，∠E=∠3，试问：AD是∠BAC的平分线吗？若是，请说明理由．
根据题意填空：
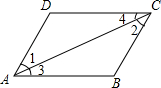根据题意填空：