题目内容
 (2013•建邺区一模)甲、乙两观光船分别从A、B两港同时出发,相向而行,两船在静水中速度相同,水流速度为5千米/小时,甲船逆流而行4小时到达B港.下图表示甲观光船距A港的距离y(千米)与行驶时间x(小时)之间的函数关系式,结合图象解答下列问题:
(2013•建邺区一模)甲、乙两观光船分别从A、B两港同时出发,相向而行,两船在静水中速度相同,水流速度为5千米/小时,甲船逆流而行4小时到达B港.下图表示甲观光船距A港的距离y(千米)与行驶时间x(小时)之间的函数关系式,结合图象解答下列问题:(1)A、B两港距离
40
40
千米,船在静水中的速度为15
15
千米/小时;(2)在同一坐标系中画出乙船距A港的距离y(千米)与行驶时间x(小时)之间的函数图象;
(3)求出发几小时后,两船相距5千米.
分析:(1)根据图形,甲4小时对应的y值即为A、B两港距离,设船在静水中的速度为x千米/小时,则逆水速度为(x-5)千米/小时,根据路程=速度×时间,列出方程求解即可;
(2)表示出乙船的速度,然后根据乙船距A港的距离等于两港的距离减去乙船形式的路程,写出y与x的函数关系式,然后作出一次函数图象即可;
(3)分相遇前相距5千米与相遇后相距5千米两种情况,根据时间=路程÷速度,列式计算即可得解.
(2)表示出乙船的速度,然后根据乙船距A港的距离等于两港的距离减去乙船形式的路程,写出y与x的函数关系式,然后作出一次函数图象即可;
(3)分相遇前相距5千米与相遇后相距5千米两种情况,根据时间=路程÷速度,列式计算即可得解.
解答:解:(1)∵x=4时,y=40,
∴A、B两港距离40千米,
设船在静水中的速度为x千米/小时,则逆水速度为(x-5)千米/小时,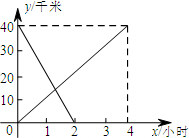
根据题意得,4(x-5)=40,
解得x=15;
(2)乙船的速度为15+5=20,
所以,乙船对应的函数解析式为y=40-20x,
当y=0时,40-20x=0,
解得x=2,
函数图象如图所示;
(3)甲船速度为:15-5=10千米/小时,
乙船速度为:15+5=20千米/小时,
若两船还没有相遇,相距5千米,则
=
小时,
若两船相遇后相距5千米,则
=
小时,
综上所述,出发
或
小时后两船相距5千米.
故答案为:40;15.
∴A、B两港距离40千米,
设船在静水中的速度为x千米/小时,则逆水速度为(x-5)千米/小时,

根据题意得,4(x-5)=40,
解得x=15;
(2)乙船的速度为15+5=20,
所以,乙船对应的函数解析式为y=40-20x,
当y=0时,40-20x=0,
解得x=2,
函数图象如图所示;
(3)甲船速度为:15-5=10千米/小时,
乙船速度为:15+5=20千米/小时,
若两船还没有相遇,相距5千米,则
| 40-5 |
| 10+20 |
| 7 |
| 6 |
若两船相遇后相距5千米,则
| 40+5 |
| 10+20 |
| 3 |
| 2 |
综上所述,出发
| 7 |
| 6 |
| 3 |
| 2 |
故答案为:40;15.
点评:本题考查了一次函数图象和实际应用相结合的问题,主要利用了静水速度、顺水速度、逆水速度、水流速度之间的关系,(3)要注意分两种情况讨论.

练习册系列答案
相关题目
 (2013•建邺区一模)如图,在直角坐标系中,直线y=2x与双曲线
(2013•建邺区一模)如图,在直角坐标系中,直线y=2x与双曲线