题目内容
 如图,任意四边形ABCD中,AC和BD相交于点O,把△AOB、△AOD、△COD、△BOC的面积分别记作S1、S2、S3、S4,则下列各式成立的是
如图,任意四边形ABCD中,AC和BD相交于点O,把△AOB、△AOD、△COD、△BOC的面积分别记作S1、S2、S3、S4,则下列各式成立的是
- A.S1+S3=S2+S4
- B.S3-S2=S4-S1
- C.S1•S4=S2•S3
- D.S1•S3=S2•S4
D
分析:作BE⊥AC于点E,从而可分别表示出S1和S2然后可得出 ,同理可得出
,同理可得出 ,这样即可证得S1•S3=S2•S4.
,这样即可证得S1•S3=S2•S4.
解答: 解:如图,过点D作DE⊥AC于点E,
解:如图,过点D作DE⊥AC于点E,
则S1= CO•DE,S2=
CO•DE,S2= AO•DE,
AO•DE,
∴ =
=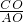 ,
,
同理可证: =
= ,
,
∴ =
= ,
,
∴S1•S3=S2•S4.
故选D.
点评:本题考查了三角形面积的求法.解答该题时,主要是抓住不同底等高三角形面积间的数量关系.
分析:作BE⊥AC于点E,从而可分别表示出S1和S2然后可得出
 ,同理可得出
,同理可得出 ,这样即可证得S1•S3=S2•S4.
,这样即可证得S1•S3=S2•S4.解答:
 解:如图,过点D作DE⊥AC于点E,
解:如图,过点D作DE⊥AC于点E,则S1=
 CO•DE,S2=
CO•DE,S2= AO•DE,
AO•DE,∴
 =
=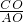 ,
,同理可证:
 =
= ,
,∴
 =
= ,
,∴S1•S3=S2•S4.
故选D.
点评:本题考查了三角形面积的求法.解答该题时,主要是抓住不同底等高三角形面积间的数量关系.

练习册系列答案
相关题目
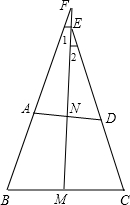 如图,任意四边形ABCD中,AB=CD,M、N分别为BC、AD的中点.说明∠1与∠2的大小关系.
如图,任意四边形ABCD中,AB=CD,M、N分别为BC、AD的中点.说明∠1与∠2的大小关系.
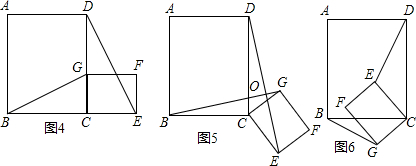
 如图,任意四边形ABCD中,AB=CD,M、N分别为BC、AD的中点.说明∠1与∠2的大小关系.
如图,任意四边形ABCD中,AB=CD,M、N分别为BC、AD的中点.说明∠1与∠2的大小关系.