题目内容
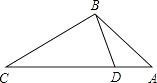
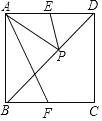
【题目】如图,△![]() 中,
中,![]() 的平分线与
的平分线与![]() 的平分线相交于点
的平分线相交于点![]() .
.
⑴.若![]() ,求
,求![]() 和
和![]() 度数;
度数;
⑵.由第⑴小题的计算,发现![]() 和
和![]() 有什么关系?它们是不是一定有这种关系?请作出说明.
有什么关系?它们是不是一定有这种关系?请作出说明.
【答案】⑴.![]() ; ⑵.
; ⑵.![]() ,理由详见解析.
,理由详见解析.
【解析】
⑴根据三角形内角和定理,已知∠ABC=60![]() ,∠ACB=40
,∠ACB=40![]() ,易求∠A和
,易求∠A和
∠D度数.
(2)根据三角形内角和定理以及角平分线性质,先求出∠D的等式,再与∠A比较即可解答.
在△![]() 中,∠ABC=60
中,∠ABC=60![]() ,∠ACB=40
,∠ACB=40![]() ,∴∠A=180
,∴∠A=180![]() -∠ABC-∠ACB=80
-∠ABC-∠ACB=80![]() ,
,
∵BD为∠ABC的角平分线,CD为∠ACE的角平分线,
∴∠DBC=![]() ∠ABC=
∠ABC=![]()
∠ACD=(180![]() -∠ACB)=
-∠ACB)=![]()
∴∠D=180![]() -∠DBC-∠ACB-∠ACD=180
-∠DBC-∠ACB-∠ACD=180![]() -30
-30![]() -40
-40![]() -70
-70![]() =40
=40![]()
∴∠A=80![]() ,∠D=40
,∠D=40![]()
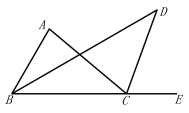
(2)通过第(1)的计算,得到∠A=2∠D,
理由如下
∵∠ACE=∠A+∠ABC
∴∠ACD+∠ECD=∠A+∠ABD+∠DBE,∠DCE=∠D+∠DBC
又BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠DBE,∠ACD=∠ECD
∴∠A=2(∠DCE-∠DBC),
∠D=∠DCE-∠DBC,
∴∠A=2∠D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目