题目内容
边长相等的正三角形和正六边形的面积之比为( )
分析:根据正三角形与正六边形的性质得出正三角形的面积以及正六边形面积进而得出两者之比即可.
解答:解:设正三角形的边长为2a,则正六边形的边长为2a;
过A作AD⊥BC于D,则∠BAD=30°,
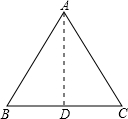
AD=AB•cos30°=2a•
=
a,
∴S△ABC=
BC•AD=
×2a×
a=
a2;
连接OA、OB,过O作OD⊥AB;

∵∠AOB=
=60°,
∴∠AOD=30°,
∴OD=OB•cos30°=2a•
=
a,
∴S△ABO=
BA•OD=
×2a×
a=
a2;
∴正六边形的面积为:6
a2;
∴边长相等的正三角形和正六边形的面积之比为:
a2:6
a2=1:6,
故选:C.
过A作AD⊥BC于D,则∠BAD=30°,

AD=AB•cos30°=2a•
| ||
| 2 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
连接OA、OB,过O作OD⊥AB;

∵∠AOB=
| 360° |
| 6 |
∴∠AOD=30°,
∴OD=OB•cos30°=2a•
| ||
| 2 |
| 3 |
∴S△ABO=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴正六边形的面积为:6
| 3 |
∴边长相等的正三角形和正六边形的面积之比为:
| 3 |
| 3 |
故选:C.
点评:此题主要考查了正三角形与正六边形的性质,根据已知利用解直角三角形知识求出正六边形面积是解题关键.

练习册系列答案
相关题目
小亮家客厅地面准备用边长相等的正三角形和正六边形地砖进行镶嵌,则在同一顶点处,正三角形地砖和正六边形地砖数目分别是( )
| A、3,2 | B、2,2 | C、4,2 | D、2,2或4,1 |