题目内容
 (2012•广安)如图,2012年4月10日,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(
(2012•广安)如图,2012年4月10日,中国渔民在中国南海黄岩岛附近捕鱼作业,中国海监船在A地侦查发现,在南偏东60°方向的B地,有一艘某国军舰正以每小时13海里的速度向正西方向的C地行驶,企图抓捕正在C地捕鱼的中国渔民,此时,C地位于中国海监船的南偏东45°方向的10海里处,中国海监船以每小时30海里的速度赶往C地救援我国渔民,能不能及时赶到?(| 2 |
| 3 |
| 6 |
分析:过点A作AD⊥BC的延长线于点D,则△ACD是等腰直角三角形,根据AC=10海里可求出AD即CD的长,在Rt△ABD中利用锐角三角函数的定义求出BD的长进而可得出BC的长,再根据中国海监船以每小时30海里的速度航行,国军舰正以每小时13海里的速度即可得出两军舰到达C点所用的时间,进而得出结论.
解答: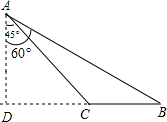 解:过点A作AD⊥BC的延长线于点D,
解:过点A作AD⊥BC的延长线于点D,
∵∠CAD=45°,AC=10海里,
∴△ACD是等腰直角三角形,
∴AD=CD=
=
=5
(海里),
在Rt△ABD中,
∵∠DAB=60°,
∴BD=AD•tan60°=5
×
=5
(海里),
∴BC=BD-CD=(5
-5
)海里,
∵中国海监船以每小时30海里的速度航行,某国军舰正以每小时13海里的速度航行,
∴海监船到达C点所用的时间t=
=
=
(小时);
某国军舰到达C点所用的时间i=
=
≈
=0.4(小时),
∵
<0.4,
∴中国海监船能及时赶到.
 解:过点A作AD⊥BC的延长线于点D,
解:过点A作AD⊥BC的延长线于点D,∵∠CAD=45°,AC=10海里,
∴△ACD是等腰直角三角形,
∴AD=CD=
|
|
| 2 |
在Rt△ABD中,
∵∠DAB=60°,
∴BD=AD•tan60°=5
| 2 |
| 3 |
| 6 |
∴BC=BD-CD=(5
| 6 |
| 2 |
∵中国海监船以每小时30海里的速度航行,某国军舰正以每小时13海里的速度航行,
∴海监船到达C点所用的时间t=
| AC |
| 30 |
| 10 |
| 30 |
| 1 |
| 3 |
某国军舰到达C点所用的时间i=
| BC |
| 13 |
5(
| ||||
| 13 |
| 5(2.45-1.41) |
| 13 |
∵
| 1 |
| 3 |
∴中国海监船能及时赶到.
点评:本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,构造出直角三角形,利用直角三角形的性质求解是解答此题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
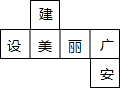 (2012•广安)如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
(2012•广安)如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( ) (2012•广安)如图,把抛物线y=
(2012•广安)如图,把抛物线y= (2012•广安)如图,已知双曲线y=
(2012•广安)如图,已知双曲线y=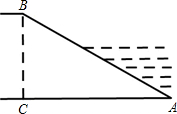 (2012•广安)如图,某水库堤坝横断面迎水坡AB的坡比是1
(2012•广安)如图,某水库堤坝横断面迎水坡AB的坡比是1