题目内容
阅读下列材料,然后回答所提出的问题.(1)
| 1 |
| 1×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5×7 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
于是
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
=
| 1 |
| 2 |
| 1 |
| 7 |
| 3 |
| 7 |
(2)上面求的方法是通过逆用分数减法法则,将和式中各分数转化为两个分数之差,使得除首末两项外的中间各项可以互相抵消,从而达到求和的目的.
通过阅读,你学会一种解决问题的方法了吗?试用学到的方法计算:
①
| 1 |
| x(x+3) |
| 1 |
| (x+3)(x+6) |
| 1 |
| (x+6)(x+9) |
②
| 1 |
| a(a+1) |
| 1 |
| (a+1)(a+2) |
| 1 |
| (a+2)(a+3) |
| 1 |
| (a+2006)(a+2007) |
分析:认真阅读材料,将每一个分式分裂为两个分式,观察抵消规律,掌握这种方法,学着使用.
解答:解:(1)原式=
(
-
)+
(
-
)+
(
-
)
=(
-
+
-
+
-
)
=
•
=
;
(2)原式=(
-
)+
(
-
)+(
-
)+…+(
-
)
=(
-
+
-
+
-
+…+
-
)
=
=
.
| 1 |
| 3 |
| 1 |
| x |
| 1 |
| x+3 |
| 1 |
| 2 |
| 1 |
| x+3 |
| 1 |
| x+6 |
| 1 |
| 3 |
| 1 |
| x+6 |
| 1 |
| x+9 |
=(
| 1 |
| x |
| 1 |
| x+3 |
| 1 |
| x+3 |
| 1 |
| x+6 |
| 1 |
| x+6 |
| 1 |
| x+9 |
=
| 1 |
| 3 |
| x+9-x |
| x(x+9) |
=
| 3 |
| x(x+9) |
(2)原式=(
| 1 |
| a |
| 1 |
| a+1 |
| 1 |
| 2 |
| 1 |
| a+1 |
| 1 |
| a+2 |
| 1 |
| a+2 |
| 1 |
| a+3 |
| 1 |
| a+2006 |
| 1 |
| a+2007 |
=(
| 1 |
| a |
| 1 |
| a+1 |
| 1 |
| a+1 |
| 1 |
| a+2 |
| 1 |
| a+2 |
| 1 |
| a+3 |
| 1 |
| a+2006 |
| 1 |
| a+2007 |
=
| a+2007-a |
| a(a+2007) |
=
| 2007 |
| a(a+2007) |
点评:此题考查了分式减法的逆运算,培养了学生灵活应用知识的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
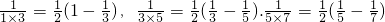 ,
,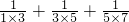
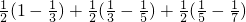
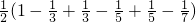
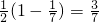 ;
;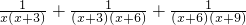 ;
;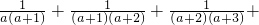 …
…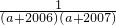 .
.