题目内容
【题目】如图,已知一次函数![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() ,与x轴相交于点B.
,与x轴相交于点B.
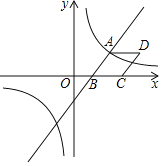
(1)求k的值;
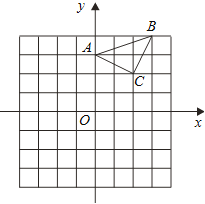
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数![]() 的图象,请直接写出:当
的图象,请直接写出:当![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
【答案】(1)12;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)把点A(4,n)代入一次函数![]() ,得到n的值为3;再把点A(4,3)代入反比例函数
,得到n的值为3;再把点A(4,3)代入反比例函数![]() ,得到k的值为12;
,得到k的值为12;
(2)根据坐标轴上点的坐标特征可得点B的坐标为(2,0),过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,根据勾股定理得到![]() ,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标;
,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标;
(3)根据反比例函数的性质即可得到当y≥-3时,自变量x的取值范围.
(1)把点![]() 代入一次函数
代入一次函数![]() ,可得
,可得![]() ;
;
把点![]() 代入反比例函数
代入反比例函数![]() ,可得
,可得![]() ,
,
解得![]() .
.
(2)∵一次函数![]() 与x轴相交于点B,令y=0,
与x轴相交于点B,令y=0,
∴![]() ,
,
解得![]() ,
,
∴点B的坐标为![]() ,
,
如图,过点A作![]() 轴,垂足为E,过点D作
轴,垂足为E,过点D作![]() 轴,垂足为F,
轴,垂足为F,

∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∵四边形ABCD是菱形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 轴,
轴,![]() 轴,
轴,
∴![]() ,
,
在![]() 与
与![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴点D的坐标为![]() .
.
(3)当y=-2时,-2=![]() ,
,
解得x=-6.
故当y≥-2时,自变量x的取值范围是x≤-6或x>0.

【题目】抛物线y=ax2+bx+c中,b=4a,它的图象如图,有以下结论:①c>0;②a+b+c>0;③a﹣b+c>0 ④b2﹣4ac<0;⑤abc<0;⑥4a>c;其中正确的为_____(填序号).
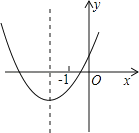
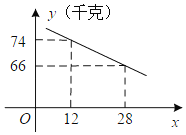
【题目】某公司销售部有营业员15人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励,为了确定一个适当的月销售目标,公司有关部门统计了这15人某月的销售量,如下表所示:
月销售量/件数 | 1770 | 480 | 220 | 180 | 120 | 90 |
人数 | 1 | 1 | 3 | 3 | 3 | 4 |
(1)直接写出这15名营业员该月销售量数据的平均数、中位数、众数;
(2)如果想让一半左右的营业员都能达到月销售目标,你认为(1)中的平均数、中位数、众数中,哪个最适合作为月销售目标?请说明理由.