题目内容
如图，在⊙O中，CD是直径，AB是弦，且CD⊥AB，已知CD=10，CM=2，求AB．分析：连结OA，先根据垂径定理由CD⊥AB得到AM=BM，再计算出OM，然后利用勾股定理计算出AM，再根据AB=2AM进行计算．
解答：
解：连结OA，如图，
∵CD⊥AB，
∴AM=BM，
∵直径CD=10，
∴OC=OA=5，
∴OM=OC-CM=5-2=3，
在Rt△OAM中，AM=
=4，
∴AB=2AM=8．
解：连结OA，如图，∵CD⊥AB，
∴AM=BM，
∵直径CD=10，
∴OC=OA=5，
∴OM=OC-CM=5-2=3，
在Rt△OAM中，AM=
| OA2-OM2 |
∴AB=2AM=8．
点评：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13、如图，在△ABC中，CD是AB边上的中线，线段AC比BC短2cm，则△BCD和△ACD的周长的差是
14、如图，在△ABC中，CD平分∠ACB，DE∥AC，DC∥EF，则与∠ACD相等角有
如图，在△ABC中，CD、BE分别是AB、AC边上的高，∠EBC=45°，BE=6，CD=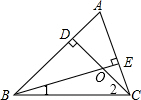
如图，在△ABC中，CD是AB边上的高，BE是AC边上的高，点O是两条高线的交点，则∠A与∠1+∠2的关系是（ ）
如图，在⊙O中，