题目内容
【题目】在等边![]() 中,点
中,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 的延长线上且
的延长线上且![]() .
.
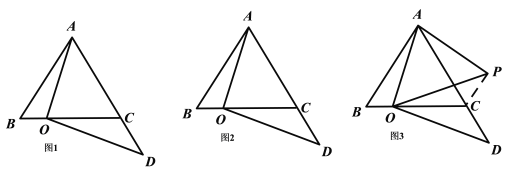
(1)如图1,若点![]() 为
为![]() 中点,求
中点,求![]() 的度数;
的度数;
(2)如图2,若点![]() 为
为![]() 上任意一点,求证
上任意一点,求证![]() .
.
(3)如图3,若点![]() 为
为![]() 上任意一点,点
上任意一点,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,连接
,连接![]() ,请判断
,请判断![]() 的形状,并说明理由.
的形状,并说明理由.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 是等边三角形,理由见解析.
是等边三角形,理由见解析.
【解析】
(1)根据三角形的等边三角形的性质可求![]() 且
且![]() ,根据
,根据![]() ,等腰三角形的性质得到
,等腰三角形的性质得到![]() 的度数,再通过内角和定理求
的度数,再通过内角和定理求![]() ,即可求出
,即可求出![]() 的度数.
的度数.
(2)过![]() 作
作![]() ,
,![]() 交
交![]() 于
于![]() 先证明
先证明![]() 为等边三角形,再根据等边三角形的性质求
为等边三角形,再根据等边三角形的性质求![]() ,
,![]() ,再证明
,再证明![]() ,得到
,得到![]() ,再通过证明得到
,再通过证明得到![]() 、
、![]() 通过,又因为
通过,又因为![]() ,通过等量代换即可得到答案.
,通过等量代换即可得到答案.
(3)通过作辅助线先证明![]() ,得到
,得到![]() ,又因为
,又因为![]() ,得到AO=OP,证得
,得到AO=OP,证得![]() 为等腰三角形,如解析辅助线,由(2)可知得
为等腰三角形,如解析辅助线,由(2)可知得![]() 得到
得到![]() ,通过角的关系得到
,通过角的关系得到![]() ,即可证得
,即可证得![]() 是等边三角形.
是等边三角形.
(1)∵![]() 为等边三角形
为等边三角形
∴![]()
∵![]() 为
为![]() 中点
中点
∴![]()
且![]()
∵![]()
∴![]() 中,
中,![]()
∴![]()
∴![]()
(2)过![]() 作
作![]() ,
,![]() 交
交![]() 于
于![]()
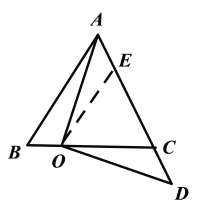
∵![]()
∴![]()
![]()
∴![]() 为等边三角形
为等边三角形
∴![]()
![]()
![]()
又∵![]()
∴![]()
在![]() 和
和![]() 中
中
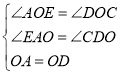
∴![]()
∴![]()
∵![]()
![]()
∴![]()
∴![]() ,
,
∵![]() ,
,![]()
∴![]()
(3)![]() 为等边三角形
为等边三角形
证明过程如下:
连接![]() ,延长
,延长![]() 交
交![]() 于
于![]()
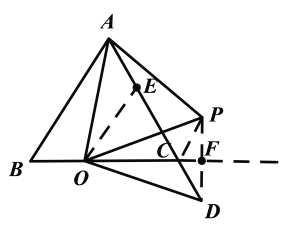
∵![]() 关于
关于![]() 对称
对称
∴![]()
在![]() 与
与![]() 中,
中,
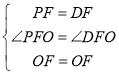
∴![]()
∴![]() ,
,![]()
∵![]()
∴AO=OP
∴![]() 为等腰三角形
为等腰三角形
过![]() 作
作![]() ,
,![]() 交
交![]() 于
于![]()
由(2)得![]()
∴![]()
又∵![]()
∴![]()
∴![]()
即![]()
∵AB∥OE,∠B=60°
∴![]()
∴![]()
∴![]() 是等边三角形.
是等边三角形.

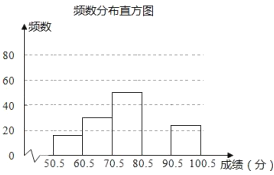
【题目】为弘扬中华传统文化,某校组织八年级800名学生参加汉字听写大赛为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,得到如下所示的模数分布表:
分数段 | 50.5~60.5 | 60.5~70.5 | 70.5~80.5 | 80.5~90.5 | 90.5~100.5 |
频数 | 16 | 30 | 50 | m | 24 |
所占百分比 | 8% | 15% | 25% | 40% | n |
请根据尚未完成的表格,解答下列问题:
(1)本次抽样调查的样本容量为_____,表中m=_____.
(2)补全图中所示的频数分布直方图.
(3)若成绩超过80分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?