题目内容
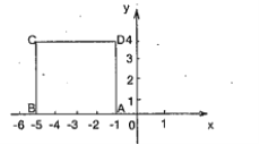
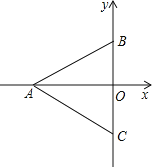
【题目】如图,等边
的顶点
,顶点
、
在
轴上．
(1)写出、两点的坐标;
(2)求的面积和周长．
【答案】（1）B（0，4） C（0，-4）；（2）
，24．
【解析】
（1）由等边三角形的性质可知原点是BC的中点，AB=2BO，在Rt△AOB中，由勾股定理可求得BO,OC的长,从而得出B,C的坐标；
（2）根据B、C的坐标求得等边三角形ABC的边长，然后根据面积公式和周长公式即可求得结果.
解：（1）∵△ABC是等边三角形，
轴⊥
轴，
∴∠BAO=30°，BO=OC，
∴AB=2BO.
在Rt△AOB中，由勾股定理得
,
又∵A（
）,∴AO=
,
∴
,
∴BO=4,∴OC=OB=4.
∴点B，C的坐标分别为B（0，4），C（0，-4）；
（2）由（1）得B（0，4），C（0，-4），
∴BC=8，
∴
=
=；
∴
.
故
的面积为，周长为24.
练习册系列答案
巧学巧练系列答案
相关题目
