题目内容
 如图所示,直线AB与射线CD平行,点E是AB上的一点,点G是CD上的一点,∠BEF=35°,FC平分∠EFG,若∠C=20°,求∠FGD的度数.
如图所示,直线AB与射线CD平行,点E是AB上的一点,点G是CD上的一点,∠BEF=35°,FC平分∠EFG,若∠C=20°,求∠FGD的度数.分析:过点F作FH∥AB,根据两直线平行,内错角相等可得∠EFH=∠BEF,∠CFH=∠C,然后求出∠CFE,再根据角平分线的定义可得∠CFG=∠CFE,再求出∠GFH,然后根据两直线平行,内错角相等可得∠FGD=∠GFH.
解答: 解:如图,过点F作FH∥AB,
解:如图,过点F作FH∥AB,
∵AB∥CD,
∴AB∥FH∥CD,
∴∠EFH=∠BEF=35°,∠CFH=∠C=20°,
∴∠CFE=∠EFH+∠CFH=35°+20°=55°,
∵FC平分∠EFG,
∴∠CFG=∠CFE=55°,
∴∠GFH=∠CFG+∠CFH=55°+20°=75°,
∵FH∥CD,
∴∠FGD=∠GFH=75°.
 解:如图,过点F作FH∥AB,
解:如图,过点F作FH∥AB,∵AB∥CD,
∴AB∥FH∥CD,
∴∠EFH=∠BEF=35°,∠CFH=∠C=20°,
∴∠CFE=∠EFH+∠CFH=35°+20°=55°,
∵FC平分∠EFG,
∴∠CFG=∠CFE=55°,
∴∠GFH=∠CFG+∠CFH=55°+20°=75°,
∵FH∥CD,
∴∠FGD=∠GFH=75°.
点评:本题考查了平行线的性质,角平分线的定义,此类题目,过拐点作平行线是解题的关键,也是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
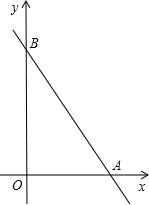 如图所示,直线AB与两坐标轴的交点坐标分别是A(6,0),B(0,8),O是坐标系原点.
如图所示,直线AB与两坐标轴的交点坐标分别是A(6,0),B(0,8),O是坐标系原点.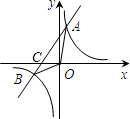 如图所示,直线AB与反比例函数
如图所示,直线AB与反比例函数 如图所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=25°,则∠BOD=
如图所示,直线AB与直线CD相交于点O,EO⊥AB,∠EOD=25°,则∠BOD= 如图所示,直线AB与CD相交于O点,∠1=∠2.若∠AOE=140°,则∠AOC 的度数为( )
如图所示,直线AB与CD相交于O点,∠1=∠2.若∠AOE=140°,则∠AOC 的度数为( ) 如图所示,直线AB与CD交于点O,∠BOD=31°36′,OE平分∠BOC,则∠AOD+∠COE=
如图所示,直线AB与CD交于点O,∠BOD=31°36′,OE平分∠BOC,则∠AOD+∠COE=