题目内容
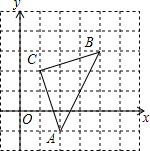如图，直角坐标系中，三角形ABC的顶点都在网格点上，其中，C点坐标为（1，2），（1）写出点A、B的坐标；
（2）求出三角形ABC的面积；
（3）若三角形A1B1C1向左平移2个单位，再向下平移2个单位，恰好得到三角形ABC，试在该直角平面坐标系中画出三角形A1B1C1．
分析：（1）根据平面直角坐标系写出点A、B的坐标即可；
（2）利用△ABC所在的矩形的面积减去四周三个直角三角形的面积列式计算即可得解；
（3）根据网格结构找出点A、B、C平移前的点A1、B1、C1的位置，然后顺次连接即可．
（2）利用△ABC所在的矩形的面积减去四周三个直角三角形的面积列式计算即可得解；
（3）根据网格结构找出点A、B、C平移前的点A1、B1、C1的位置，然后顺次连接即可．
解答：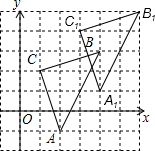
解：（1）A（2，-1），B（4，3）；
（2）△ABC的面积=3×4-
×1×3-
×2×4-
×1×3
=12-1.5-4-1.5
=12-7
=5；
（3）△A1B1C1如图所示．
解：（1）A（2，-1），B（4，3）；（2）△ABC的面积=3×4-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=12-1.5-4-1.5
=12-7
=5；
（3）△A1B1C1如图所示．
点评：本题考查了利用平移变换作图，三角形的面积，熟练掌握网格结构准确找出对应点的位置是解题的关键．
练习册系列答案
相关题目
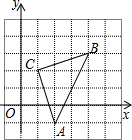如图，直角坐标系中，△ABC的顶点都在网格点上，其中，A点坐标为（2，-1），则△ABC的面积为
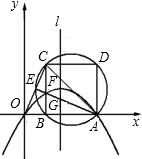？若存在，请求出所有这样的点；若不存在，请说明理由．
在如图平面直角坐标系中，△ABC三个顶点A、B、C的坐标分别为A（2，-1），B（1，-3），C（4，-4），
如图，直角坐标系中，△ABC的顶点都在网格点上，C点坐标为（1，2），原来△ABC各个顶点纵坐标不变，横坐标都增加2，所得的三角形面积是
在如图的直角坐标系中，将△ABC平移后得到△A′B′C′，它们的个顶点坐标如表所示：