题目内容
阅读下列材料并填空：
（1）探究：平面上有n个点（n≥2）且任意3个点不在同一条直线上，经过每两点画一条直线，一共能画多少条直线？
我们知道，两点确定一条直线．平面上有2个点时，可以画
条直线，平面内有3个点时，一共可以画
条直线，平面上有4个点时，一共可以画
条直线，平面内有5个点时，一共可以画_____条直线，…平面内有n个点时，一共可以画_______条直线；
（2）迁移：某足球比赛中有n个球队（n≥2）进行单循环比赛（每两队之间必须比赛一场），一共要进行多少场比赛？
有2个球队时，要进行
场比赛，有3个球队时，要进行
场比赛，有4个球队时，要进行_______场比赛，…那么有20个球队时，要进行______场比赛。
（1）探究：平面上有n个点（n≥2）且任意3个点不在同一条直线上，经过每两点画一条直线，一共能画多少条直线？
我们知道，两点确定一条直线．平面上有2个点时，可以画
条直线，平面内有3个点时，一共可以画条直线，平面上有4个点时，一共可以画条直线，平面内有5个点时，一共可以画_____条直线，…平面内有n个点时，一共可以画_______条直线；（2）迁移：某足球比赛中有n个球队（n≥2）进行单循环比赛（每两队之间必须比赛一场），一共要进行多少场比赛？
有2个球队时，要进行
场比赛，有3个球队时，要进行场比赛，有4个球队时，要进行_______场比赛，…那么有20个球队时，要进行______场比赛。解：（1）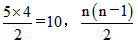
；
（2）
。
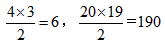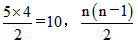；（2）
。
练习册系列答案
天天向上一本好卷系列答案
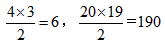小学生10分钟应用题系列答案
相关题目
阅读下列材料并填空．
平面上有n个点（n≥2）且任意三个点不在同一条直线上，过其中的每两点画直线，一共能作出多少条不同的直线？
①分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线…
②归纳：考察点的个数和可连成直线的条数Sn发现：如下表
③推理：平面上有n个点，两点确定一条直线．取第一个点A有n种取法，取第二个点B有（n-1）种取法，所以一共可连成n（n-1）条直线，但AB与BA是同一条直线，故应除以2；即Sn=
④结论：Sn=
试探究以下几个问题：平面上有n个点（n≥3），任意三个点不在同一条直线上，过任意三个点作三角形，一共能作出多少不同的三角形？
（1）分析：
当仅有3个点时，可作出 个三角形；
当仅有4个点时，可作出 个三角形；
当仅有5个点时，可作出 个三角形；
…
（2）归纳：考察点的个数n和可作出的三角形的个数Sn，发现：（填下表）
（3）推理：
（4）结论：
平面上有n个点（n≥2）且任意三个点不在同一条直线上，过其中的每两点画直线，一共能作出多少条不同的直线？
①分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线…
②归纳：考察点的个数和可连成直线的条数Sn发现：如下表
| 点的个数 | 可作出直线条数 | ||
| 2 | 1=S2=
| ||
| 3 | 3=S3=
| ||
| 4 | 6=S4=
| ||
| 5 | 10=S5=
| ||
| … | … | ||
| n | Sn=
|
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
（1）分析：
当仅有3个点时，可作出
当仅有4个点时，可作出
当仅有5个点时，可作出
…
（2）归纳：考察点的个数n和可作出的三角形的个数Sn，发现：（填下表）
| 点的个数 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| … | |
| n |
（4）结论：
、阅读下列材料并填空。平面上有n个点（n≥2）且任意三个点不在同一条直线上，过这些点作直线，一共能作出多少条不同的直线？
①分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线……
②归纳：考察点的个数和可连成直线的条数
发现：如下表
| 点的个数 | 可作出直线条数 |
| 2 | 1= |
| 3 | 3= |
| 4 | 6= |
| 5 | 10= |
| …… | …… |
| n |
|
③推理：平面上有n个点，两点确定一条直线。取第一个点A有n种取法，取第二个点B有（n－1）种取法，所以一共可连成n(n-1)条直线，但AB与BA是同一条直线，故应除以2；即
④结论：
试探究以下几个问题：平面上有n个点（n≥3），任意三个点不在同一条直线上，过任意三个点作三角形，一共能作出多少不同的三角形？
（1）分析：
当仅有3个点时，可作出 个三角形；
当仅有4个点时，可作出 个三角形；
当仅有5个点时，可作出 个三角形；
……
（2）归纳：考察点的个数n和可作出的三角形的个数，发现：（填下表）
| 点的个数 | 可连成三角形个数 |
| 3 |
|
| 4 |
|
| 5 |
|
| …… |
|
| n |
|
(3)推理：
（4）结论：
+
=5
－
=x-6