题目内容
有2条生产线计划在一个月(30天)内组装520台产品(每天产品的产量相同),按原先的组装速度,不能完成任务;若加班生产,每条生产线每天多组装2台产品,能提前完成任务.
(1)每条生产线原先每天最多能组装多少台产品?
(2)要按计划完成任务,策略一:增添1条生产线,共要多投资19000元;策略二:按每天能组装最多台数加班生产,每条生产线每天共要多花费350元;选哪一个策略较省费用?
解:(1)每条生产线原先每天最多能组装x台产品,根据题意可得
 ,
,
解得:15<x<17,
∵x的值应是整数,
∴x最大为17.
答:每条生产线原先每天最多能组装17台产品.
(2)策略一:增添1条生产线,共要多投资19000元;
策略二:520÷19×350×2≈28×350×2=19600元;
所以策略一较省费用.

练习册系列答案
相关题目
已知点A的坐标为(2,0),点P在直线y=x上运动,当以点P为圆心,PA的长为半径的圆的面积最小时,点P的坐标为( )
|
| A. | (1,﹣1) | B. | (0,0) | C. | (1,1) | D. | ( |

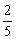 ;若往盒中再放
;若往盒中再放 进1个黑球,这时取得黑球的概率变为
进1个黑球,这时取得黑球的概率变为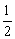 .
. ,
, |﹣3tan30°.
|﹣3tan30°. ,其中
,其中 .
.