题目内容
一工人在定期内要制造出一定数量的同样零件,若他每天多做10个,则提前4| 1 | 2 |
分析:做本题的关键是首先设出未知数,然后根据条件“若他每天做10个,则提前4
天完成”列出表示这个工人需要做的零件个数的等式;再根据“若他每天少做5个,则要误期3天”这个条件再列出表示这个工人需要做的零件个数的等式,再根据方程组解答即可.
| 1 |
| 2 |
解答:解:分析若直接设这个工人要做x个零件,定期为y天,则他每天做
一个零件,根据题目条件,若他每天多做10个,则可以减少4
天工期,所以,
x=(
+10)(y-4
)
另一方面,如果他每天少做5个,则要增加3天工期,因此,
x=(
-5)(y+3),
显然,将此两式联立,解出x,y即可.
设工人要做x个零件,定期为y天,则他每天做x/y个,依分析有方程组
整理得
②×2+①得
=50, x=50y
将x=50y代入②得
y=27,x=50 y=1350,即
答:工人要做1350个零件,定期为27天.
| x |
| y |
| 1 |
| 2 |
x=(
| x |
| y |
| 1 |
| 2 |
另一方面,如果他每天少做5个,则要增加3天工期,因此,
x=(
| x |
| y |
显然,将此两式联立,解出x,y即可.
设工人要做x个零件,定期为y天,则他每天做x/y个,依分析有方程组
|
整理得
|
②×2+①得
| x |
| y |
将x=50y代入②得
y=27,x=50 y=1350,即
|
答:工人要做1350个零件,定期为27天.
点评:此题主要考查了根据实际问题找等量关系列方程,解方程的问题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
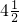 天完成,若他每天少做5个,则要误期3天.问他要做多少个零件?定期是多少天?
天完成,若他每天少做5个,则要误期3天.问他要做多少个零件?定期是多少天?