题目内容
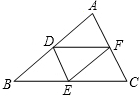 如图D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD得△DEF,如果△ABC的周长是36cm,那么△DEF的周长是
如图D、E、F分别是△ABC的边AB、BC、CA的中点,连接DE、EF、FD得△DEF,如果△ABC的周长是36cm,那么△DEF的周长是18cm
18cm
.分析:利用三角形的中位线定理可以得到:DE=
AC,EF=
AB,DF=
BC,则△DEF的周长是△ABC的周长的一半,据此即可求解.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵D、E分别是△ABC的边AB、BC的中点,
∴DE=
AC,
同理,EF=
AB,DF=
BC,
∴C△DEF=DE+EF+DF=
AC+
BC+
AB=
(AC+BC+AC)=
×36=18cm.
故答案是:18cm.
∴DE=
| 1 |
| 2 |
同理,EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴C△DEF=DE+EF+DF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案是:18cm.
点评:本题考查了三角形的中位线定理,正确根据三角形中位线定理证得:△DEF的周长是△ABC的周长的一半是关键.

练习册系列答案
相关题目
 甲、乙分别从A地、B地同时相向而行.他们离开A地的路程y(km/h) 和行走的时间x(h)之间的函数关系如图所示,解析式分别是y1=4x和y2=-3x+6.
甲、乙分别从A地、B地同时相向而行.他们离开A地的路程y(km/h) 和行走的时间x(h)之间的函数关系如图所示,解析式分别是y1=4x和y2=-3x+6.
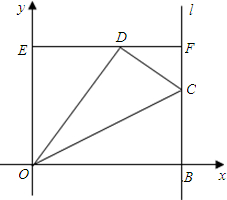 ,S△DOH:S△DHC=1:4,求G点坐标.
,S△DOH:S△DHC=1:4,求G点坐标.