题目内容
已知抛物线 ,
,
【小题1】(1)若 ,
, ,求该抛物线与
,求该抛物线与 轴公共点的坐标;
轴公共点的坐标;
【小题2】(2)若 ,且当
,且当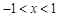 时,抛物线与
时,抛物线与 轴有且只有一个公共点,求
轴有且只有一个公共点,求 的取值范围;
的取值范围;
【小题3】(3)若 ,且
,且 时,对应的
时,对应的 ;
; 时,对应的
时,对应的 ,试判断当
,试判断当 时,抛物线与
时,抛物线与 轴是否有公共点?若有,有几个,证明你的结论;若没有,阐述理由.
轴是否有公共点?若有,有几个,证明你的结论;若没有,阐述理由.
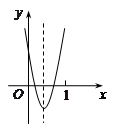
【小题1】(Ⅰ)当 ,
, 时,抛物线为
时,抛物线为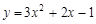 ,
,
方程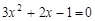 的两个根为
的两个根为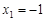 ,
,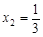 .
.
∴该抛物线与 轴公共点的坐标是
轴公共点的坐标是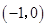 和
和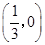 . 1
. 1
【小题2】(Ⅱ)当 时,抛物线为
时,抛物线为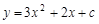 ,且与
,且与 轴有公共点.
轴有公共点.
对于方程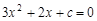 ,判别式
,判别式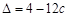 ≥0,有
≥0,有 ≤
≤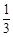 .·································· 2’
.·································· 2’
①当 时,由方程
时,由方程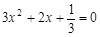 ,解得
,解得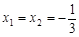 .
.
此时抛物线为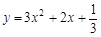 与
与 轴只有一个公共点
轴只有一个公共点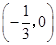 .····························· 3’
.····························· 3’
②当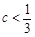 时,
时,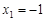 时,
时, ,
, 时,
时,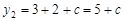 .
.
由已知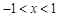 时,该抛物线与
时,该抛物线与 轴有且只有一个公共点,考虑其对称轴为
轴有且只有一个公共点,考虑其对称轴为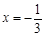 ,
,
应有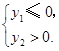 即
即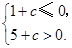
解得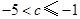 .
.
综上, 或
或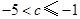 . 4’
. 4’
【小题3】(3)对于二次函数 ,
,
由已知 时,
时,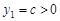 ;
; 时,
时,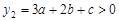 ,
,
又 ,∴
,∴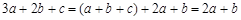 .
.
于是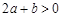 .而
.而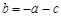 ,∴
,∴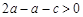 ,即
,即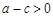 .
.
∴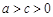 . ·························································································· 5’
. ·························································································· 5’
∵关于 的一元二次方程
的一元二次方程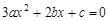 的判别式
的判别式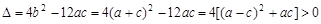 ,
,
∴抛物线 与
与 轴有两个公共点,顶点在
轴有两个公共点,顶点在 轴下方.·························· 6’
轴下方.·························· 6’
又该抛物线的对称轴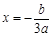 ,
,
由 ,
,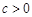 ,
,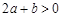 ,
,
得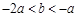 ,
,
∴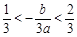 . ...………………………………………….7’
. ...………………………………………….7’
又由已知 时,
时, ;
; 时,
时, ,观察图象,
,观察图象,
可知在 范围内,该抛物线与
范围内,该抛物线与 轴有两个公共点. 8’
轴有两个公共点. 8’
解析

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 。【小题1】<1>求抛物线顶点M的坐标;
。【小题1】<1>求抛物线顶点M的坐标; ,
, 轴的交点坐标;
轴的交点坐标; 时,抛物线与
时,抛物线与 .
. .
.