题目内容
如图.以O为圆心的圆与△AOB的边AB相切于点C.与OB相交于点D,且OD=BD,己知sinA=| 2 |
| 5 |
| 21 |
 (1)求⊙O的半径:
(1)求⊙O的半径:(2)求图中阴影部分的面枳.
分析:(1)根据切线的性质得出CO⊥AB,再根据解直角三角形得出CO,AO的关系,进而得出它们的长度,即可得出半径长度;
(2)根据已知得出∠COD=60°,进而利用三角形面积减去扇形面积即可得出答案.
(2)根据已知得出∠COD=60°,进而利用三角形面积减去扇形面积即可得出答案.
解答: 解:(1)连接OC,
解:(1)连接OC,
∵以O为圆心的圆与△AOB的边AB相切于点C.
∴CO⊥AB,
∵sinA=
=
,
∵AC=
.
∴假设CO=2x,AO=5x,
4x2+21=25x2,
解得:x=1,
∴CO=2,
∴⊙O的半径为2;
(2)∵⊙O的半径为2,
∴DO=2,
∵DO=DB,
∴BO=4,
∴BC=2
,
∴2CO=BO,
∵OC⊥BC,
∴∠CBO=30°,
∠COD=60°,
图中阴影部分的面枳为:S△OCB-S扇形COD=
×2
×2-
=2
-
π.
 解:(1)连接OC,
解:(1)连接OC,∵以O为圆心的圆与△AOB的边AB相切于点C.
∴CO⊥AB,
∵sinA=
| 2 |
| 5 |
| CO |
| AO |
∵AC=
| 21 |
∴假设CO=2x,AO=5x,
4x2+21=25x2,
解得:x=1,
∴CO=2,
∴⊙O的半径为2;
(2)∵⊙O的半径为2,
∴DO=2,
∵DO=DB,
∴BO=4,
∴BC=2
| 3 |
∴2CO=BO,
∵OC⊥BC,
∴∠CBO=30°,
∠COD=60°,
图中阴影部分的面枳为:S△OCB-S扇形COD=
| 1 |
| 2 |
| 3 |
| 60π×22 |
| 360 |
| 3 |
| 2 |
| 3 |
点评:此题主要考查了扇形面积求法以及切线的性质和勾股定理的应用等知识,得出图中阴影部分的面枳为:S△OCB-S扇形COD是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
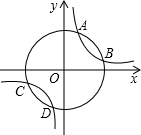 如图,以原点为圆心的圆与反比例函数y=
如图,以原点为圆心的圆与反比例函数y=| 3 |
| x |
| A、-3 | B、-2 | C、-1 | D、-4 |

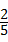 ,AC=
,AC= .
.
 的图象交于
的图象交于 、
、 、
、 、
、 四点,已知点
四点,已知点
 B.
B. C.
C. D.
D.