题目内容
 如图,已知一次函数y=x+1的图象与反比例函数y=
如图,已知一次函数y=x+1的图象与反比例函数y=| k | x |
分析:由于△AOB的面积为1,根据反比例函数的比例系数k的几何意义可知k=2,解由y=x+1与y=
联立起来的方程组,得出A点坐标,又易求点C的坐标,从而利用勾股定理求出AC的长.
| k |
| x |
解答:解:∵点A在反比例函数y=
的图象上,AB⊥x轴于点B,△AOB的面积为1,
∴k=2.
解方程组
,
得
,
.∴A(1,2);
在y=x+1中,令y=0,得x=-1.∴C(-1,0).
∴AB=2,BC=2,
∴AC=
=2
.
| k |
| x |
∴k=2.
解方程组
|
得
|
|
在y=x+1中,令y=0,得x=-1.∴C(-1,0).
∴AB=2,BC=2,
∴AC=
| 22+22 |
| 2 |
点评:本题考查函数图象交点坐标的求法及反比例函数的比例系数k与其图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S=
|k|.
| 1 |
| 2 |

练习册系列答案
相关题目
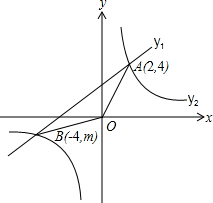 B(-4,m)两点.
B(-4,m)两点. 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=- (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数 如图,已知一次函数y=kx+b的图象交反比例函数
如图,已知一次函数y=kx+b的图象交反比例函数