Question

（2012•永春县模拟）已知Rt△AOB的两条直角边OA=3，OB=1，分别以OA、OB所在直线为x轴、y轴建立平面直角坐标系，如图所示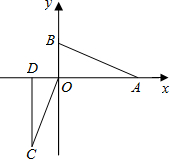．先将Rt△AOB绕原点O按顺时针方向旋转90°后，再沿x轴负方向平移1个单位长度得到△CDO．
（1）直接写出点A、C的坐标；
（2）求线段AB扫过的图形的面积．

Answer 1

分析：（1）利用Rt△AOB的两条直角边OA=3，OB=1，得出DO=1，CD=3，即可得出C点坐标与A点坐标；
（2）利用AB扫过的图形的面积包括以AO为半径90°圆心角组成的扇形-以BO为半径90°为圆心角的扇形+S_△A′B′O+S_△OCA′，进而得出面积即可．

解答：解：（1）∵Rt△AOB的两条直角边OA=3，OB=1，
∴A点坐标为：（3，0），DO=1，CD=3，
∴C点坐标为：（-1，-3）（4分）；

（2）如图所示：AB扫过的图形的面积=以AO为半径90°圆心角组成的扇形-以BO为半径90°为圆心角的扇形+S_△A′B′O+S_△OCA′，
=

90π (32-12)

360

+

1

2

×1×3+

1

2

×1×3=2π+3（9分）．

点评：此题主要考查了坐标与图形的旋转与平移和图形面积求法，解答此题的关键是明确AB扫过的图形的面积包括以AO为半径90°圆心角组成的扇形-以BO为半径90°为圆心角的扇形+S_△ABO+S_△OCA′．