Question

（1）探索：如果把一个多面体的顶点数记为V，棱数记为E，面数记为F，填写下表．

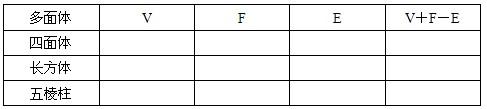
多面体	V	F	E	V+F-E
四面体
长方体
五棱柱

（2）猜想：由上面的探究你能得到一个什么结论？
（3）验证：再找出一个多面体，数一数它有几个顶点，几条棱，几个面，看看面数、顶点数、棱数是否满足上述关系．
（4）应用（2）的结论对所有的多面体都成立，伟大的数学家欧拉证明了这个关系式，上述关系式叫做欧拉公式．根据欧拉公式，想一想会不会有一个多面体，它有10个面，30条棱，20个顶点？

Answer 1

（1）

多面体	V	F	E	V+F-E
四面体	4	4	6	2
长方体	8	6	12	2
五棱柱	10	7	15	2

（2）V+F-E=2；

（3）例如六棱柱，有顶点数为12，面数为8，棱数为18，12+8-18=2符合上述关系，所以满足；

（4）∵不满足欧拉公式，∴不可能．
分析：（1）四面体为三棱锥，顶点数为4，面数为4，棱数为6，V+F-E=2；长方体的顶点数为8，面数为6，棱数为12，V+F-E=2；五棱柱的顶点数为10，面数为7，棱数为15，V+F-E=2；
（2）由（1）可得V+F-E为一个定值，恒为2；
（3）例如六棱柱，有顶点数为12，面数为8，棱数为18，12+8-18=2符合上述关系；
（4）10+20-30不等于2，所以不会有．
点评：本题考查几何体面数，顶点数，棱数之间的关系．