Question

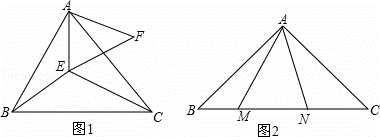
（1）如图所示，△ABC和△AEF为等边三角形，点E在△ABC内部，且E到点A、B、C的距离分别为3、4、5，求∠AEB的度数．

（2）如图2，在△ABC中，∠CAB=90°，AB=AC，M、N为BC上的两点，且∠MAN=45°，MN²与NC²+BM²有何关系？请证明你的结论．

Answer 1

       （1）解：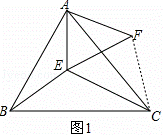

连接FC，

∵△ABC和△AEF为等边三角形，

∴AE=AF=EF=3，AB=AC，∠AFE=60°，∠BAC=∠EAF=60°，

∴∠BAE=∠CAF=60°﹣∠CAE，

在△BAE和△CAF中

∴△BAE≌△CAF，

∴CF=BE=4，∠AEB=∠AFC，

∴EF=3，CE=5，

∴CE²=EF²+CF²，

∴∠CFE=90°

∵∠AFE=60°，

∴∠AFC=90°+60°=150°，

∴∠AEB=∠AFC=150°；

（2）MN²=NC²+BM²，

证明：将△ABM绕A点逆时钟选择90，得到△AFC，

则AM=AF，CF=BM，∠BAM=∠CAF，∠B=∠ACF，

∵∠BAC=90°，∠MAN=45°，

∴∠NAF=∠CAN+∠FAC=∠CAN+∠BAM=90°﹣45°=45°=∠MAN，

在△MAN和△FAN中

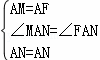
∴△MAN≌△FAN，

∴MN=FN，

∵∠BAC=90°，AB=AC，

∴∠B=∠ACB=45°，

∵∠B=∠ACF，

∴∠ACF=45°，

∴∠FCN=90°，

由勾股定理得：NF²=CF²+CN²，

∵CF=BM，NF=MN，

∴MN²=NC²+BM²．