Question

【题目】已知AD是△ABC的中线P是线段AD上的一点（不与点A、D重合），连接PB、PC，E、F、G、H分别是AB、AC、PB、PC的中点，AD与EF交于点M；

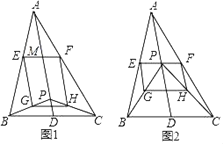
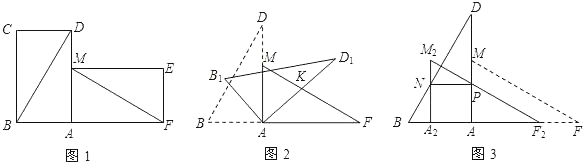
（1）如图1，当AB＝AC时，求证：四边形EGHF是矩形；

（2）如图2，当点P与点M重合时，在不添加任何辅助线的条件下，写出所有与△BPE面积相等的三角形（不包括△BPE本身）．

Answer 1

【答案】（1）见解析；（2）△APE、△APF、△CPF、△PGH．

【解析】

（1）由三角形中位线定理得出EG∥AP，EF∥BC，EF=BC，GH∥BC，GH=BC，推出EF∥GH，EF=GH，证得四边形EGHF是平行四边形，证得EF⊥AP，推出EF⊥EG，即可得出结论；

（2）由△APE与△BPE的底AE=BE，又等高，得出S△APE=S△BPE，由△APE与△APF的底EP=FP，又等高，得出S△APE=S△APF，由△APF与△CPF的底AF=CF，又等高，得出S△APF=S△CPF，证得△PGH底边GH上的高等于△AEF底边EF上高的一半，推出S△PGH=S△AEF=S△APF，即可得出结果．

（1）证明：∵E、F、G、H分别是AB、AC、PB、PC的中点，

∴EG∥AP，EF∥BC，EF＝BC，GH∥BC，GH＝BC，

∴EF∥GH，EF＝GH，

∴四边形EGHF是平行四边形，

∵AB＝AC，

∴AD⊥BC，

∴EF⊥AP，

∵EG∥AP，

∴EF⊥EG，

∴平行四边形EGHF是矩形；

（2）∵PE是△APB的中线，

∴△APE与△BPE的底AE＝BE，又等高，

∴S△APE＝S△BPE，

∵AP是△AEF的中线，

∴△APE与△APF的底EP＝FP，又等高，

∴S△APE＝S△APF，

∴S△APF＝S△BPE，

∵PF是△APC的中线，

∴△APF与△CPF的底AF＝CF，又等高，

∴S△APF＝S△CPF，

∴S△CPF＝S△BPE，

∵EF∥GH∥BC，E、F、G、H分别是AB、AC、PB、PC的中点，

∴△AEF底边EF上的高等于△ABC底边BC上高的一半，△PGH底边GH上的高等于△PBC底边BC上高的一半，

∴△PGH底边GH上的高等于△AEF底边EF上高的一半，

∵GH＝EF，

∴S△PGH＝S△AEF＝S△APF，

综上所述，与△BPE面积相等的三角形为：△APE、△APF、△CPF、△PGH．