题目内容
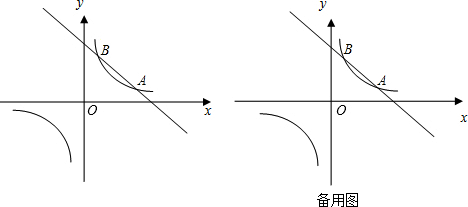
(2011•德宏州)如图,已知直线y=ax+b(a≠0)与双曲线y=
(k≠0)交于A、B两点,且点A(2,1),点B的纵坐标为2.
(1)求双曲线的解析式;
(2)求直线的解析式;
(3)求线段AB的长;
(4)问在双曲线上是否存在点C,使△ABC的面积等于3?若存在,求出点C的坐标;若不存在,说明理由(结果不需要分母有理化)
| k | x |
(1)求双曲线的解析式;
(2)求直线的解析式;
(3)求线段AB的长;
(4)问在双曲线上是否存在点C,使△ABC的面积等于3?若存在,求出点C的坐标;若不存在,说明理由(结果不需要分母有理化)

分析:(1)将点A的坐标代入双曲线解析式,即可求得k的值;
(2)把点B的纵坐标代入(1)中的双曲线解析式即可求得点B的横坐标;然后把点A、B的坐标分别代入直线方程,列出关于a、b的方程组,通过解方程组来求a、b的值;
(3)利用两点间的距离公式来求线段AB的长度;
(4)如图,过点C作CD∥x轴,交直线AB于点D;过点C作CH⊥AB于点H.利用面积法求得CH=3
.然后根据反比例函数图象上点的坐标特征设C(x,
),则D(3-
,
).
易求|CD|=|3-
-x|=6;最后通过解绝对值方程来求x的值.
(2)把点B的纵坐标代入(1)中的双曲线解析式即可求得点B的横坐标;然后把点A、B的坐标分别代入直线方程,列出关于a、b的方程组,通过解方程组来求a、b的值;
(3)利用两点间的距离公式来求线段AB的长度;
(4)如图,过点C作CD∥x轴,交直线AB于点D;过点C作CH⊥AB于点H.利用面积法求得CH=3
| 2 |
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
易求|CD|=|3-
| 2 |
| x |
解答:解:(1)根据题意知,点A(2,1)在双曲线y=
(k≠0)上,则k=xy=2×1=2,
所以双曲线的解析式为y=
;
(2)根据题意知,点B在双曲线y=
上,且点B的纵坐标是2.故设B(x,2).则
2=
,
解得,x=1,
故点B的坐标是(1,2).
∵点A、B都在直线y=ax+b(a≠0)上,
∴
,
解得,
,
∴直线的解析式为:y=-x+3;
(3)∵A(2,1),B(1,2),
∴AB=
=
,即线段AB的长度是
;
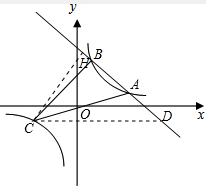
(4)存在,理由如下:
如图,过点C作CD∥x轴,交直线AB于点D;过点C作CH⊥AB于点H.
∵AB=
,S△ABC=3,
∴
AB•CH=3,即
×
=3,
∴CH=3
.
设C(x,
),则D(3-
,
).
∴|CD|=|3-
-x|.
在Rt△CDH中,∠CDB=45°,CH=3
,则CD=6,
得方程|3-
-x|=6.
①当3-
-x=6时,解得,x1=-1,x2=-2,
∴点C的坐标是(-1,-2),(-2,-1);
②当3-
-x=-6时,解得x1=
,x2=
,
∴点C的坐标是(
,
),(
,
);
综上所述,符号条件的点C有4个,即(-1,-2),(-2,-1),(
,
),(
,
).
| k |
| x |
所以双曲线的解析式为y=
| 2 |
| x |
(2)根据题意知,点B在双曲线y=
| 2 |
| x |
2=
| 2 |
| x |
解得,x=1,
故点B的坐标是(1,2).
∵点A、B都在直线y=ax+b(a≠0)上,
∴
|
解得,
|
∴直线的解析式为:y=-x+3;
(3)∵A(2,1),B(1,2),
∴AB=
| (1-2)2+(2-1)2 |
| 2 |
| 2 |

(4)存在,理由如下:
如图,过点C作CD∥x轴,交直线AB于点D;过点C作CH⊥AB于点H.
∵AB=
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
∴CH=3
| 2 |
设C(x,
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
∴|CD|=|3-
| 2 |
| x |
在Rt△CDH中,∠CDB=45°,CH=3
| 2 |
得方程|3-
| 2 |
| x |
①当3-
| 2 |
| x |
∴点C的坐标是(-1,-2),(-2,-1);
②当3-
| 2 |
| x |
9+
| ||
| 2 |
9-
| ||
| 2 |
∴点C的坐标是(
9+
| ||
| 2 |
| 4 | ||
9+
|
9-
| ||
| 2 |
| 4 | ||
9-
|
综上所述,符号条件的点C有4个,即(-1,-2),(-2,-1),(
9+
| ||
| 2 |
| 4 | ||
9+
|
9-
| ||
| 2 |
| 4 | ||
9-
|
点评:本题考查了反比例函数与一次函数的交点问题.用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
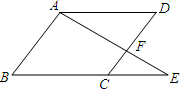 (2011•德宏州)如图,在平行四边形ABCD中,延长BC到点E,使CE:BC=1:2,连接AE交CD于点F,则S△FCE:S△ABE=
(2011•德宏州)如图,在平行四边形ABCD中,延长BC到点E,使CE:BC=1:2,连接AE交CD于点F,则S△FCE:S△ABE=