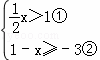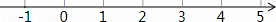题目内容
如图,射线PA切⊙O于点A,连接PO.
(1)在PO的上方作射线PC,使∠OPC=∠OPA(用尺规在原图中作,保留痕迹,不写作法),并证明:PC是⊙O的切线;
(2)在(1)的条件下,若PC切⊙O于点B,AB=AP=4,求 的长.
的长.

解:(1)作图如右图,
连接OA,过O作OB⊥PC,
∵PA切⊙O于点A,
∴OA⊥PA,
又∵∠OPC=∠OPA,OB⊥PC,
∴OA=OB,即d=r,
∴PC是⊙O的切线;
(2)∵PA、PC是⊙O的切线,
∴PA=PB,
又∵AB=AP=4,
∴△PAB是等边三角形,
∴∠APB=60°,
∴∠AOB=120°,∠POA=60°,
在Rt△AOP中,tan60°=
∴OA=
∴ =
= =
= .
.


练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
国家统计局数据显示,截至2014年末全国商品房待售面积约为62200万平方米,该数据用科学记数法可表示为( )
|
| A. | 6.22×104 | B. | 6.22×107 | C. | 6.22×108 | D. | 6.22×109 |
中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为( )
|
| A. | 44×108 | B. | 4.4×109 | C. | 4.4×108 | D. | 4.4×1010 |
 中自变量
中自变量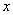 的取值范围是
的取值范围是 C.x≥-3或
C.x≥-3或