题目内容
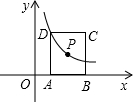 如图,已知正方形ABCD的边AB在x轴的正半轴上,点C、D在第一象限内,点P是正方形ABCD的对称中心,反比例函数
如图,已知正方形ABCD的边AB在x轴的正半轴上,点C、D在第一象限内,点P是正方形ABCD的对称中心,反比例函数 (k>0)的图象经过点D、P,若A的坐标是(1,0),则k=________.
(k>0)的图象经过点D、P,若A的坐标是(1,0),则k=________.
2
分析:根据点P是正方形ABCD的对称中心,假设正方形边长为x,得出AQ= ,PQ=
,PQ= ,再根据反比例函数的性质xy=k,得出x的值,即可得出k的值.
,再根据反比例函数的性质xy=k,得出x的值,即可得出k的值.
解答: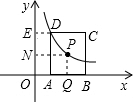 解:作PQ⊥BO,PN⊥y轴,DE⊥y轴,
解:作PQ⊥BO,PN⊥y轴,DE⊥y轴,
∵点P是正方形ABCD的对称中心,假设正方形边长为x,
∴AQ= ,PQ=
,PQ= ,
,
∴P点的坐标为(1+ ,
, ),D点的坐标为(1,x),
),D点的坐标为(1,x),
∵图象经过点D、P点,
(1+ )×
)× =1×x,
=1×x,
解得:x=2或0(不合题意舍去),
∴P点的坐标为:(2,1)
∴k=xy=1×2=2,
故答案为:2.
点评:此题主要考查了反比例函数的性质,用x表示出P,D点的坐标是解决问题的关键.
分析:根据点P是正方形ABCD的对称中心,假设正方形边长为x,得出AQ=
 ,PQ=
,PQ= ,再根据反比例函数的性质xy=k,得出x的值,即可得出k的值.
,再根据反比例函数的性质xy=k,得出x的值,即可得出k的值.解答:
 解:作PQ⊥BO,PN⊥y轴,DE⊥y轴,
解:作PQ⊥BO,PN⊥y轴,DE⊥y轴,∵点P是正方形ABCD的对称中心,假设正方形边长为x,
∴AQ=
 ,PQ=
,PQ= ,
,∴P点的坐标为(1+
 ,
, ),D点的坐标为(1,x),
),D点的坐标为(1,x),∵图象经过点D、P点,
(1+
 )×
)× =1×x,
=1×x,解得:x=2或0(不合题意舍去),
∴P点的坐标为:(2,1)
∴k=xy=1×2=2,
故答案为:2.
点评:此题主要考查了反比例函数的性质,用x表示出P,D点的坐标是解决问题的关键.

练习册系列答案
相关题目
 如图,已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上,直线BE与DM交于点N.求证:BN⊥DM.
如图,已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上,直线BE与DM交于点N.求证:BN⊥DM. (2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上. 如图,已知正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的值是( )
如图,已知正方形ABCD的对角线交于O,过O点作OE⊥OF,分别交AB、BC于E、F,若AE=4,CF=3,则EF的值是( ) 如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.