题目内容
(2011•梅州)如图,在平面直角坐标系中,点A(-4,4),点B(-4,0),将△ABO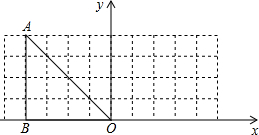 绕原点O按顺时针方向旋转135°得到△A1B1O.回答下列问题:(直接写结果)
绕原点O按顺时针方向旋转135°得到△A1B1O.回答下列问题:(直接写结果)
(1)∠AOB=
(2)顶点A从开始到A1经过的路径长为
(3)点B1的坐标为
 绕原点O按顺时针方向旋转135°得到△A1B1O.回答下列问题:(直接写结果)
绕原点O按顺时针方向旋转135°得到△A1B1O.回答下列问题:(直接写结果)(1)∠AOB=
45
45
°;(2)顶点A从开始到A1经过的路径长为
3
π
| 2 |
3
π
;| 2 |
(3)点B1的坐标为
(2
,2
)
| 2 |
| 2 |
(2
,2
)
.| 2 |
| 2 |
分析:(1)根据点的坐标知△AOB为等腰直角三角形;
(2)求OA的长度,根据弧长公式求解;
(3)根据等腰直角三角形的性质和旋转到的位置求解.
(2)求OA的长度,根据弧长公式求解;
(3)根据等腰直角三角形的性质和旋转到的位置求解.
解答: 解:(1)∵在平面直角坐标系中,点A(-4,4),点B(-4,0),
解:(1)∵在平面直角坐标系中,点A(-4,4),点B(-4,0),
∴AB=OB=4,∠ABO=90°.
∴∠AOB=45°,OA=
=4
;
(2)
的长度l=
=3
π;
(3)设OA的中点为C,连接BC.
则BC⊥OA.BC=OC=
OA=2
.
∴B1的横纵坐标相等,OB1=4,
∴根据旋转的性质知点B1的坐标为(2
,2
).
故答案为:(1)45;(2)3
π;(3)(2
,2
).
 解:(1)∵在平面直角坐标系中,点A(-4,4),点B(-4,0),
解:(1)∵在平面直角坐标系中,点A(-4,4),点B(-4,0),∴AB=OB=4,∠ABO=90°.
∴∠AOB=45°,OA=
| AB2+OB2 |
| 2 |
(2)
 |
| AA′ |
135×4
| ||
| 180 |
| 2 |
(3)设OA的中点为C,连接BC.
则BC⊥OA.BC=OC=
| 1 |
| 2 |
| 2 |
∴B1的横纵坐标相等,OB1=4,
∴根据旋转的性质知点B1的坐标为(2
| 2 |
| 2 |
故答案为:(1)45;(2)3
| 2 |
| 2 |
| 2 |
点评:此题考查旋转的性质、弧长的计算、等腰直角三角形的性质等知识点,难度中等.

练习册系列答案
相关题目
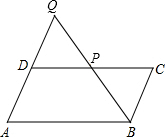 (2011•梅州)如图,点P在平行四边形ABCD的CD边上,连接BP并延长与AD的延长线交于点Q.
(2011•梅州)如图,点P在平行四边形ABCD的CD边上,连接BP并延长与AD的延长线交于点Q.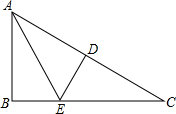 (2011•梅州)如图,在 Rt△ABC中,∠B=90°.ED是AC的垂直平分线,交AC于点D,交BC于点E,已知∠BAE=30°,则∠C的度数为
(2011•梅州)如图,在 Rt△ABC中,∠B=90°.ED是AC的垂直平分线,交AC于点D,交BC于点E,已知∠BAE=30°,则∠C的度数为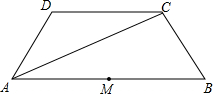 边AB的中点M重合.
边AB的中点M重合.