题目内容
已知关于x的方程kx2-(3k-1)x+2k-2=0.
(1)判断命题:“无论k为何值,方程总有两个实数根”的真假,如果是真命题,请给出证明;如果是假命题请举一次反例.
(2)若k≠0,设方程的两个实数根分别为x1,x2(其中x1<x2),当k的取值范围满足什么条件时,有x1(1-x2)+x2< 成立?
成立?
解:(1)“无论x取何值,方程总有两个实数根”是假命题,
反例:当k=0时,原式可化为x-2=0,解得x=2,只有一个实数根.
(2)∵k≠0,
∴x1+x2= ,x1•x2=
,x1•x2= ,
,
又∵x1(1-x2)+x2< ,
,
∴x1+x2-x1•x2= -
- =
= =
=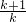 ,
,
于是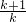 <
< ,
,
①当k>0时,k2-2k-2>0,解得k<1- (舍去)或k>1+
(舍去)或k>1+ ;
;
②当k<0时,k2-2k-2>0,k取任意实数.
综上所述,k>1+ 或k<0.
或k<0.
分析:(1)由于k的取值范围不确定,可知kx2-(3k-1)x+2k-2=0可能为一元二次方程,也可能为一元一次方程,当其为一元一次方程时,只有一个实数根.
(2)由于k≠0,可知方程为一元二次方程,先求出两根之和与两根之积的表达式,再代入x1(1-x2)+x2< 解答.
解答.
点评:本题考查了根的判别式、根与系数的关系、命题与定理、反证法,综合性较强.
反例:当k=0时,原式可化为x-2=0,解得x=2,只有一个实数根.
(2)∵k≠0,
∴x1+x2=
 ,x1•x2=
,x1•x2= ,
,又∵x1(1-x2)+x2<
 ,
,∴x1+x2-x1•x2=
 -
- =
= =
=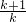 ,
,于是
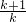 <
< ,
,①当k>0时,k2-2k-2>0,解得k<1-
 (舍去)或k>1+
(舍去)或k>1+ ;
;②当k<0时,k2-2k-2>0,k取任意实数.
综上所述,k>1+
 或k<0.
或k<0.分析:(1)由于k的取值范围不确定,可知kx2-(3k-1)x+2k-2=0可能为一元二次方程,也可能为一元一次方程,当其为一元一次方程时,只有一个实数根.
(2)由于k≠0,可知方程为一元二次方程,先求出两根之和与两根之积的表达式,再代入x1(1-x2)+x2<
 解答.
解答.点评:本题考查了根的判别式、根与系数的关系、命题与定理、反证法,综合性较强.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 -kx-6=0的一个根为3,则实数k的值为(
)
-kx-6=0的一个根为3,则实数k的值为(
)