题目内容
如图,在⊙O中, |
| BC |
 |
| BD |
 |
| CD |
(1)请你在图中过点B作⊙O的切线AE,并证明AE∥CD;
(不写作法,作图允许使用三角板)
(2)求证:MC•MD=MF•MB;
(3)如图,若点M是
 |
| BC |
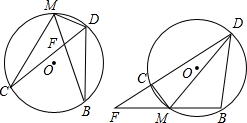 延长线交于点F,连接MC,MD,BD,则结论MC•MD=MF•MB是否仍然成立?如果成立,请写出证明过程;如果不成立,请说明理由.
延长线交于点F,连接MC,MD,BD,则结论MC•MD=MF•MB是否仍然成立?如果成立,请写出证明过程;如果不成立,请说明理由.
分析:(1)当作出切线AE后,弦切角DBE和弧BD(弧BC)∠BMC相等,又∠BMC和∠BDC为同弧所对的圆周角,所以有∠DBE=∠BMC=∠BDC,所以AE∥CD;
(2)因为∠DBM和∠DCM为同弧所对的圆周角,所以相等,又∠BMD和∠BMC为等弧所对的圆周角,所以相等,即△MCF∽△MBD则有MC•MD=MF•MB;
(3)四边形BDCM是⊙O的内接四边形,所以有∠FMC=∠BDC,∠FCM=∠B,又因为∠BDC和∠BMD为等弧所对的圆周角,所以相等,两组对应角相等,所以相似.
(2)因为∠DBM和∠DCM为同弧所对的圆周角,所以相等,又∠BMD和∠BMC为等弧所对的圆周角,所以相等,即△MCF∽△MBD则有MC•MD=MF•MB;
(3)四边形BDCM是⊙O的内接四边形,所以有∠FMC=∠BDC,∠FCM=∠B,又因为∠BDC和∠BMD为等弧所对的圆周角,所以相等,两组对应角相等,所以相似.
解答: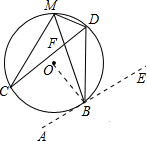 解:(1)如图,正确作出切线.
解:(1)如图,正确作出切线.
证明:∵AE是⊙O的切线,
∴∠DBE=∠DMB.
∵
=
,
∴∠CDB=∠DMB.
∴∠DBE=∠CDB.
∴AE∥CD.
(2)证明:∵
=
,
∴∠CMF=∠BMD.
又∵∠MCF=∠MBD,
∴△MCF∽△MBD.
∴
=
.
∴MC•MD=MF•MB.
(3)成立.
证明:∵四边形BDCM是⊙O的内接四边形,
∴∠FCM=∠DBM,∠FMC=∠BDC.
∵
=
,
∴∠BDC=∠DMB.
∴∠FMC=∠DMB.
∴△MCF∽△MBD.
∴
=
.
∴MC•MD=MF•MB.
 解:(1)如图,正确作出切线.
解:(1)如图,正确作出切线.证明:∵AE是⊙O的切线,
∴∠DBE=∠DMB.
∵
 |
| BC |
 |
| BD |
∴∠CDB=∠DMB.
∴∠DBE=∠CDB.
∴AE∥CD.
(2)证明:∵
 |
| BC |
 |
| BD |
∴∠CMF=∠BMD.
又∵∠MCF=∠MBD,
∴△MCF∽△MBD.
∴
| MC |
| MB |
| MF |
| MD |
∴MC•MD=MF•MB.
(3)成立.
证明:∵四边形BDCM是⊙O的内接四边形,
∴∠FCM=∠DBM,∠FMC=∠BDC.
∵
 |
| BC |
 |
| BD |
∴∠BDC=∠DMB.
∴∠FMC=∠DMB.
∴△MCF∽△MBD.
∴
| MC |
| MB |
| MF |
| MD |
∴MC•MD=MF•MB.
点评:此题主要考查了圆中等弧同弧所对的圆周角相等这一性质,以及相似的判定,难易程度适中.

练习册系列答案
相关题目
 19、如图,在△ABC中,BC边上的垂直平分线交AC于点D;已知AB=3,AC=7,BC=8,则△ABD的周长为
19、如图,在△ABC中,BC边上的垂直平分线交AC于点D;已知AB=3,AC=7,BC=8,则△ABD的周长为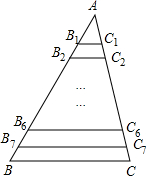 如图,在△ABC中,BC=8,B1、B2、…、B1,C1、C2、…、C7分别是AB、AC的8等分点,则B1C1+B2C2+…+B7C7的值是( )
如图,在△ABC中,BC=8,B1、B2、…、B1,C1、C2、…、C7分别是AB、AC的8等分点,则B1C1+B2C2+…+B7C7的值是( )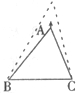 14、如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是( )
14、如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是( )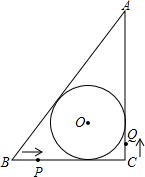 拓展探索.
拓展探索.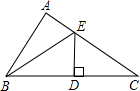 如图,在△ABC中,BC边上的垂直平分线DE交BC于点D,交AC于点E,△ABC的周长为18cm,△ABE的周长为10cm,则BD的长为
如图,在△ABC中,BC边上的垂直平分线DE交BC于点D,交AC于点E,△ABC的周长为18cm,△ABE的周长为10cm,则BD的长为