题目内容
（2012•中山二模）已知：如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．以AB边上一点O为圆心，过A、D两点作⊙O（不写作法，保留作图痕迹），再判断直线BC与⊙O的位置关系，并说明理由．分析：作出AD的垂直平分线交AB于点O，再利用切线的判定方法求出∠ODB=90°进而得出BC为⊙O的切线．
解答：
解：作图正确（需保留线段AD中垂线的痕迹）．
直线BC与⊙O相切．
理由如下：
连接OD，
∵OA=OD，∴∠OAD=∠ODA．
∵AD平分∠BAC，∴∠OAD=∠DAC．
∴∠ODA=∠DAC．∴OD∥AC．
∵∠C=90°，∴∠ODB=90°，
即OD⊥BC．
∴BC为⊙O的切线．
解：作图正确（需保留线段AD中垂线的痕迹）． 直线BC与⊙O相切．
理由如下：
连接OD，
∵OA=OD，∴∠OAD=∠ODA．
∵AD平分∠BAC，∴∠OAD=∠DAC．
∴∠ODA=∠DAC．∴OD∥AC．
∵∠C=90°，∴∠ODB=90°，
即OD⊥BC．
∴BC为⊙O的切线．
点评：此题主要考查了复杂作图以及切线的判定，利用角平分线的性质得出OD∥AC是解题关键．
练习册系列答案
相关题目
（2012•中山二模）如图所示的几何体的正视图是（ ）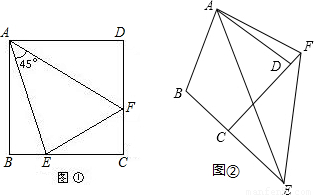
（2012•中山二模）如图1，在正方形ABCD中，E、F分别是BC，CD上的点，且∠EAF=45度．则有结论EF=BE+FD成立；