Question

【题目】如图，已知直角坐标平面上的ΔABC，AC=CB，∠ACB=90°，且A(-1，0)，B(m，n)，C(3，0)．若抛物线经过A、C两点．

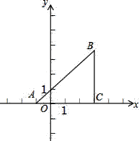
(1)求a、b的值；

(2)将抛物线向上平移若干个单位得到的新抛物线恰好经过点B，求新抛物线的解析式.

Answer 1

【答案】（1）；（2）.

【解析】

（1）只需把点A、C的坐标代入抛物线的解析式就可解决问题；

（2）可设新抛物线的解析式为y=x2-2x-3+k，然后求出点B的坐标，并把点B的坐标代入新抛物线的解析式，就可解决问题；

(1)∵抛物线经过A(-1，0)、C(3，0)，

∴，

解得：；

(2)设抛物线向上平移个单位后得到的新抛物线恰好经过点B，

则新抛物线的解析式为，

∵A(-1，0)、C(3，0)，

∴CB=AC=3-(-1)=4，

∵∠ACB=90°，

∴点B的坐标为(3，4)．

∵点B(3，4)在抛物线上，

∴，

解得：，

∴新抛物线的解析式为.