Question

【题目】已知：在中，，点在上，连接，.

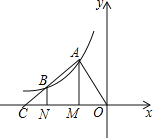
（1）如图1，求证：；

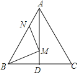
（2）如图2，点为的中点，过点作的垂线分别交的延长线，的延长线，于点，求证：；

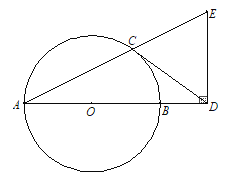
（3）如图3，在（2）的条件下，过点分别作于点于点，若，，求的面积.

Answer 1

【答案】(1)见解析；（2）见解析；（3）30

【解析】

（1）设，根据条件以及外角性质可得∠ADB=∠C+∠CAD=45°，所以，，

由三角形内角和定理可得，从而求解；

（2）过点作于点，过点作的延长线于点，可证，利用AAS证明，得出，再利用AAS证明即可证明；

（3）连接，由ASA易证 ，所以， ，因为 ，所以，又因为

所以，因为，所以

（1）证明：如图1 令，∵，∠ADB=∠C+∠CAD=45°，

∴，

在中 ∵

∴=2（45°-α ）

∴

（2）如图2 过点作于点，过点作的延长线于点

∵

∴

∴

∴

在和中

∴

∴

由（1）得，

∵HG⊥AF，

∴∠BGT=∠AHG=∠CHR，

在和中

∴

∴

（3）如图3 连接

在和中

∴

∴

∵

∴

∴

∵

∴

∵

∴