题目内容
【题目】某公司有A、B两种型号的客车，它们的载客量、每天的租金如表所示：
A型号客车 | B型号客车 | |
载客量(人/辆) | 30 | 45 |
租金(元/辆) | 450 | 600 |
已知某中学计划租用
两种型号的客车共10辆送七年级师生去某地参加社会实践活动，已知该中学租车的总费用不超过5600元.
(1)求最多能租用多少辆B型号客车？
(2)若七年级师生共有380人，请写出所有可能的租车方案.
【答案】(1)最多能租用7辆
型号客车；(2)有两种租车方案，方案一：租
型号客车4辆、型号客车6辆；方案二：租型号客车3辆、型号客车7辆.
【解析】
（1）设租用B型号客车x辆，则租用A型号客车（10-x）辆，根据总租金=600×租用B型号客车的辆数+450×租用A型号客车的辆数结合租车的总费用不超过5600元，即可得出关于x的一元一次不等式，解之即可得出x的取值范围，再取其中的最大整数值即可得出结论；
（2）设租用B型号客车x辆，则租用A型号客车（10-x）辆，根据座位数=45×租用B型号客车的辆数+30×租用A型号客车的辆数结合师生共有380人，即可得出关于x的一元一次不等式，解之即可得出x的取值范围，再结合（1）的结论及x为整数，即可得出各租车方案．
(1)设租用型号客车
辆，则租用型号客车
辆，
依题意，得：
，
解得：
又∵为整数，
∴的最大值为7.
答：最多能租用7辆型号客车.
(2)设租用型号客车辆，则租用型号客车辆，
依题意，得：
，
解得：
又∵为整数，且，
∴
.
∴有两种租车方案，方案一：租型号客车4辆、型号客车6辆；方案二：租型号客车3辆、型号客车7辆.
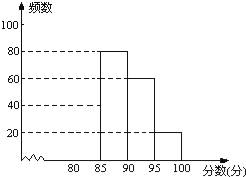
【题目】某校组织了“安全在我心中”知识竞赛活动．根据获奖同学在竞赛中的成绩制成的统计图表如下：
分数段 | 频数 | 频率 |
80≤x＜85 | x | 0.2 |
85≤x＜90 | 80 | y |
90≤x＜95 | 60 | 0.3 |
95≤x＜100 | 20 | 0.1 |
根据以上图表提供的信息，解答下列问题：
（1）写出表中x，y的数值；
（2）请补全频数分布直方图；
（3）如果成绩在95分以上（含95分）的可以获得特等奖，那么获奖的同学获得特等奖的概率是多少？
（4）获奖成绩的中位数落在哪个分数段？
