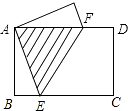
��Ŀ����
����Ŀ����ͼ���ԡ�ABCֽƬ�������²����� ��1�β���������ABC���Ź�AB�е�D1��ֱ���۵���ʹ��A����BC���ϵ�A1�����ۺ�D1E1��BC�ľ������h1 �� Ȼ��ԭֽƬ��
��2�β���������AD1E1���Ź�AD1�е�D2��ֱ���۵���ʹ��A����D1E1���ϵ�A1�����ۺ�D1E1��BC�ľ������h2 �� Ȼ��ԭֽƬ��
��
�������������ϲ�����ȥ����������n�β�����õ����ۺ�DnEn��BC�ľ������hn �� ��h=1����hn��ֵ�������ǣ� ��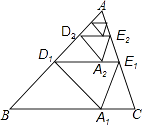
A.![]()
B.![]()
C.![]()
D.![]()
���𰸡�C
���������⣺����AA1 �� ���۵������ʿɵã�AA1��DE��DA=DA1 ��
�֡�D��AB�е㣬
��DA=DB��
��DB=DA1 ��
���BA1D=��B��
���ADA1=2��B��
�֡ߡ�ADA1=2��ADE��
���ADE=��B��
��DE��BC��
��AA1��BC��
��AA1=2��
��h1=2��1=1��
ͬ����h2=2�� ![]() ��h3=2��
��h3=2�� ![]() ��
��
�ྭ����n�β�����õ����ۺ�Dn��1En��1��BC�ľ���hn=2�� ![]() ��
��
��hn��ֵ�������� ![]() ��
��
��ѡC��
�����㾫����������Ҫ�����˷��۱任���۵����⣩�����֪ʶ�㣬��Ҫ�����۵���һ�ֶԳƱ任����������Գƣ��Գ����Ƕ�Ӧ������ߵĴ�ֱƽ���ߣ��۵�ǰ��ͼ�ε���״�ʹ�С���䣬λ�ñ仯����Ӧ�ߺͽ���Ȳ�����ȷ�����⣮