题目内容
如图,菱形ABCD中,CF⊥AD,垂足为E,交BD的延长线于F.求证:AO2=BO•OF.

【答案】
先证CO=AO,∠FCB=∠FED=900,
又CO⊥BF,
∴AO2=BO·OF.
【解析】由菱形的性质可知∠ADO=∠FDE,直角AOD和FED,则⊿ADO∽⊿FDE,可得∠DFE=∠DAO,而菱形ABCD,则∠DAO=∠OAB,即∠OAB=∠OFC,那么直角三角形OAB和OFC相似,OF/OA=OC/OB,菱形ABCD中,OA=OC,可知结论。

练习册系列答案
相关题目
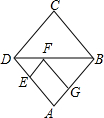 如图菱形ABCD中,EF∥AB,FG∥AD,BF:FD=m:n,CD=15,则EF+FG的长为( )
如图菱形ABCD中,EF∥AB,FG∥AD,BF:FD=m:n,CD=15,则EF+FG的长为( )| A、mn | B、15 | C、6m+9n | D、不能确定,但与m、n的取值有关 |
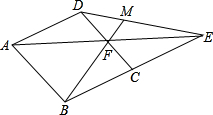 如图菱形ABCD中,∠ABC=120°,F是DC的中点,AF的延长线交BC的延长线于E,则直线BF与直线DE所夹的锐角的度数为( )
如图菱形ABCD中,∠ABC=120°,F是DC的中点,AF的延长线交BC的延长线于E,则直线BF与直线DE所夹的锐角的度数为( )| A、30° | B、40° | C、50° | D、60° |
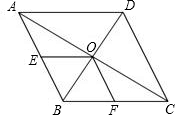
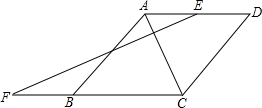 如图菱形ABCD中,点E是AD的中点,EF⊥AC交CB的延长线于点F,交AC于点M,想一想:AB与EF是否互相平分,并说明理由.
如图菱形ABCD中,点E是AD的中点,EF⊥AC交CB的延长线于点F,交AC于点M,想一想:AB与EF是否互相平分,并说明理由.