Question

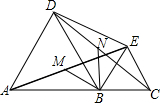（2006•海珠区一模）已知线段AC上有一动点B，分别以AB、BC为边向线段的同一侧作等边三角形△ABD和△BCE．连接AE、CD（如图），若MN分别为AE、CD的中点，
（1）求证：AM=CN；
（2）求∠MBN的大小；
（3）若连接MN，请你尽可能多的说出图中相似三角形和全等三角形．

Answer 1

分析：（1）根据等边三角形性质得出AB=BD，BC=BE，∠EBC=∠ABC=60°，求出∠ABE=∠DBC，证△ABE≌△DBC，推出AE=DC；
（2）根据全等得出∠EAB=∠CDB，证△AMB≌△DNB，推出∠ABM=∠DBN，求出∠DBN+∠MBD=60°即可；
（3）根据全等三角形的判定和相似三角形的判定定理，结合图形即可得出答案．

解答：（1）证明：∵△ABD和△BCE是等边三角形，
∴AB=BD，BC=BE，∠EBC=∠ABC=60°，
∴∠ABE=∠DBC，
在△ABE和△DBC中

AB=BD ∠ABE=∠DBC BE=BC

   
∴△ABE≌△DBC（SAS）
∴AE=DC，
∵M、N分别为AE、CD的中点，
∴AM=

1

2

AE，CN=

1

2

DC
∴AM=CN；

（2）解：∵△ABE≌△DBC，
∴∠EAB=∠CDB，
在△AMB和△DNB中

AM=DN ∠MAB=∠NDB AB=DB

  
∴△AMB≌△DNB（SAS），
∴∠ABM=∠DBN，
∵∠ABC=∠ABM+∠MBD=60°，
∴∠DBN+∠MBD=60°，
即∠MBN=60°；

（3）解：图中的全等三角形有：△ABM≌△DBN，△BME≌△BCN，△ABE≌△DBC；
相似三角形有：△ABD∽△BCE，△ABD∽△BMN，△BMN∽△BCE．

点评：本题考查了等边三角形的性质，全等三角形的性质和判定，相似三角形的性质和判定等知识点的应用．