题目内容
【题目】已知点
和点
是双曲线
上两点，
点的坐标为
，如果该双曲线上一点
使得以
、
、、为顶点的四边形是梯形，则点的坐标为__________．
【答案】
，
，
．
【解析】
根据已知条件先求出
，
，
，再对梯形的底边进行分类讨论：当梯形以
为底时，不合题意；当梯形以
为底时，求得
；当梯形以
为底时，求得
、
．
解：∵点
和点
是双曲线
上两点
∴
，解得：
∴，
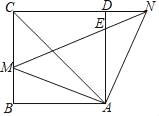
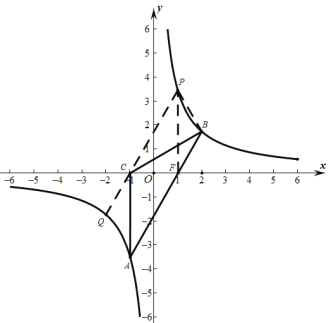
如图所示，连接，，，过
作
轴，交
轴于点
；
∴
，
∴在
中，
．
∴
①当梯形以为底时，由于过点且平行于的直线与双曲线只有一个交点，不符合题意．
②当梯形以为底时，过
作的平行线，交双曲线与点
．
过作
于
，设
∵
，
∴
∴
∴
将坐标代入双曲线解析式：
解得
或
（舍）
所以，此时
，满足要求
③当梯形以为底时，过
作的平行线，与双曲线第一象限交于点，第三象限交于点
．如图，过作
轴交轴于点
，设
∵
∴
∴
∴
∴
∴
将坐标代入双曲线解析式：
解得：
，或
（舍）
所以，此时
，满足要求；
同理可求得
，此时
，满足要求；
综⊥所述，坐标可为，，．
故答案是：，，．
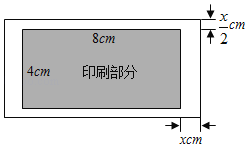
【题目】商场销售某种冰箱，该种冰箱每台进价为2500元．已知原销售价为每台2900元时，平均每天能售出8台．若在原销售价的基础上每台降价50元，则平均每天可多售出4台．设每台冰箱的实际售价比原销售价降低了x元．
（1）填表（不需化简）：
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
（2）商场为使这种冰箱平均每天的销售利润达到5000元，则每台冰箱的实际售价应定为多少元？
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究，探究过程如下，请补充完整：
(1)自变量x的取值范围是全体实数，x与y的几组对应值列表如下：
x | … | ﹣3 |
| ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中，m= ．
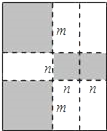
(2)根据表中数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分．
(3)探究函数图象发现：
①函数图象与x轴有 个交点，所以对应的方程x2﹣2|x|=0有 个实数根；
②方程x2﹣2|x|=
有 个实数根；
③关于x的方程x2﹣2|x|=a有4个实数根时，a的取值范围是 ．
