题目内容

有下列条件：①∠A+∠B=∠C；②∠A：∠B：∠C=1：2：3；③∠A=90°-∠B；④∠A=
1
2
∠B=
1
3
∠C．能确定△ABC是直角三角形的条件有（　　）
分析：根据直角三角形的判定对各个条件进行分析，从而得到答案．
解答：解：A、∠A+∠B=∠C=90°，△ABC是直角三角形，故本选项正确；
B、∠A：∠B：∠C=1：2：3，则∠A=30°，∠B=60°，∠C=90°，△ABC是直角三角形，故本选项正确；
C、∵∠A+∠B=90°，∴∠C=90°，△ABC是直角三角形，故本选项正确；
D、设∠A=x，∠B=2x，∠C=3x，则x+2x+3x=180°，解得x=30°，故3x=90°，△ABC是直角三角形，故本选项正确．
故选D．
点评：本题考查的是三角形内角和定理，熟知三角形的内角和等于180°是解答此题的关键．
练习册系列答案
相关题目
在△ABC和△A1B1C1中，有下列条件：①
AB
A1B1
=
BC
B1C1
，②
BC
B1C1
=
AC
A1C1
，③∠A=∠A1，④∠B=∠B1，⑤∠C=∠C1，如果从中任取两个条件组成一组，那么能判断△ABC∽△A1B1C1的有（　　）
A、4组B、5组C、6组D、7组
（2012•孝感模拟）在△ABC与△A′B′C′中，有下列条件：（1）
AB
A′B′
=
BC
B′C′
；（2）
BC
B′C′
=
AC
A′C′
；（3）∠A=∠A′；（4）∠C=∠C′．如果从中任取两个条件组成一组，那么能判断△ABC∽△A′B′C′的共有多少组（　　）
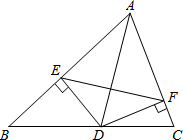如图，在△ABC中，E、F分别是AB、AC上的点．有下列条件：①AD平分∠BAC；②DE⊥AB，DF⊥AC；③AD⊥EF，以此三个中的两个作为命题的条件，另一个作为命题的结论，构成三个命题：①②?③；①③?②；②③?①．
（1）以上三个命题中，属于真命题的是
①②?③或②③?①
①②?③或②③?①
．
（2）请选择一个真命题进行证明命题（先写出所选命题，然后证明）．
在△ABC与△A′B′C′中，有下列条件：①
AB
A′B′
=
BC
B′C′
；（2）
AC
A′C′
=
BC
B′C′
③∠A=∠A′④∠C=∠C′．如果从中任取两个条件组成一组，那么能判断△ABC∽△A′B′C′的共有
 
组．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网