��Ŀ����
����Ŀ����ͼ���߳�Ϊ3������![]() �Ķ���
�Ķ���![]() ��ԭ���غϣ���
��ԭ���غϣ���![]() ��
��![]() �ᣬ
�ᣬ![]() ���ϡ�����������
���ϡ�����������![]() ��ͼ��
��ͼ��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() .
.
��1�����������Ľ���ʽ��
��2������![]() ��
��![]() ���ƽ����
���ƽ����![]() ����
����![]() ��ֱ��
��ֱ��![]() ���˶�����
���˶�����![]() ��
��![]() �����˶�.
�����˶�.
����![]() ����
����![]() Ϊֱ�Ƕ���ĵ���ֱ�������Σ���
Ϊֱ�Ƕ���ĵ���ֱ�������Σ���![]() �������
�������
�������١��е�����![]() Ϊֱ�Ƕ������ȥ�����������Ϊ����
Ϊֱ�Ƕ������ȥ�����������Ϊ����![]() �ǵ���ֱ������������
�ǵ���ֱ������������![]() ������������١�����õĽ���⣬��������______.��ֱ��д�𰸣�����д���裩
������������١�����õĽ���⣬��������______.��ֱ��д�𰸣�����д���裩
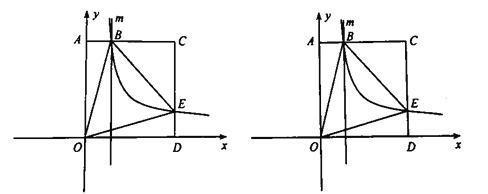
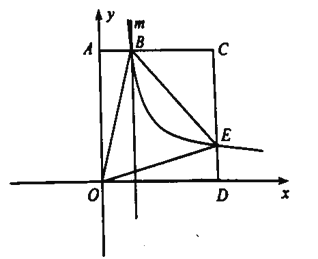
���𰸡���1��![]() ����2����
����2����![]() ��
��![]() .��5��17.
.��5��17.
��������
��1����![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() �����������ε�������������̼��ɽ�����⣮
�����������ε�������������̼��ɽ�����⣮
��2���ٷ��������λ���ͼ�Σ�����P���߶�BM�ϣ�����P���߶�BM���ӳ�����ʱ���ֱ�����ȫ�������ε�������⼴�ɣ�
�ڵ���Q�ǵ��������ε�ֱ�Ƕ���ʱ�����������ηֱ���⼴�ɣ�
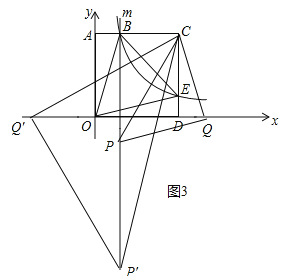
�⣺��1�������ı���OACD�������Σ��߳�Ϊ3��
���B��������Ϊ3����E�ĺ�����Ϊ3��
�߷���������![]() ��ͼ��AC��CD�ڵ�B��E��
��ͼ��AC��CD�ڵ�B��E��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() .
.
��S��OBE=4��
�ɵã�![]() .
.
��ã�![]() ��
��![]() ���ᣩ.
���ᣩ.
���ԣ������������Ľ���ʽΪ![]() .
.
��2��������ͼ1�У���ֱ��m��OD��M��
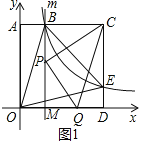
�ɣ�1����֪B��1��3����AB=1��BC=2��
��PC=PQ����CPQ=90��ʱ��
�ߡ�CBP=��PMQ=��CPQ=90����
���CPB+��BCP=90������CPB+��PQM=90����
���PCB=��MPQ����PC=PQ��
���CBP�ա�PMQ��AAS����
��BC=PM=2��PB=MQ=1��
��PC=PQ=![]()
��S��PCQ=![]()
��ͼ2�У���PQ=PC����CPQ=90����
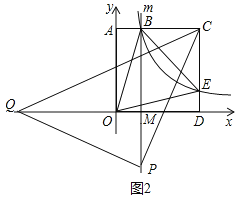
ͬ���ɵ���CBP�ա�PMQ��AAS����
��PM=BC=2��OM=PB=5��
��PC=PQ=![]() ��
��
��S��PCQ=![]() .
.
���ԣ�![]() �����Ϊ
�����Ϊ![]() ��
��![]() .
.
�ڵ���Q�ǵ��������ε�ֱ�Ƕ���ʱ��ͬ���ɵ�CQ=PQ=![]() ����ʱS��PCQ=5��
����ʱS��PCQ=5��
��CQ��=PQ��=![]() ���ɵ�S��P��CQ��=17��
���ɵ�S��P��CQ��=17��
�����ڵ�CΪ���������ε�ֱ�Ƕ��㣬
������������CPQ�������������������õĽ���⣬��������5��17��
�ʴ�Ϊ5��17��