题目内容
已知四边形ABCD的对角线AC，BD相交于点O，且OA=OC，OB=OD，则下列结论不一定成立的是
- A.AB∥CD
- B.∠BAD=∠DCB
- C.BD=AC
- D.AD=BC
C
分析：根据性质可以推出此四边形ABCD为平行四边形，然后根据平行四边形的即可推出A、B、D三项．
解答：∵四边形ABCD的对角线AC，BD相交于点O，且OA=OC，OB=OD，
∴四边形ABCD为平行四边形，
∴AB∥CD，∠BAD=∠DCB，AD=BC．
所以，A、B、D三项均成立，
故选择C
点评：本题主要考查平行四边形的判定和性质，关键在于根据：若四边形的对角线互相平分，则此四边形为平行四边形这一判定定理判定四边形ABCD为平行四边形．
分析：根据性质可以推出此四边形ABCD为平行四边形，然后根据平行四边形的即可推出A、B、D三项．
解答：∵四边形ABCD的对角线AC，BD相交于点O，且OA=OC，OB=OD，
∴四边形ABCD为平行四边形，
∴AB∥CD，∠BAD=∠DCB，AD=BC．
所以，A、B、D三项均成立，
故选择C
点评：本题主要考查平行四边形的判定和性质，关键在于根据：若四边形的对角线互相平分，则此四边形为平行四边形这一判定定理判定四边形ABCD为平行四边形．
练习册系列答案
作业辅导系列答案
同步学典一课多练系列答案
经典密卷系列答案
金牌课堂练系列答案
相关题目
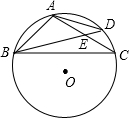如图，已知四边形ABCD的外接圆⊙O的半径为2，对角线AC与BD的交点为E，AE=EC，AB=
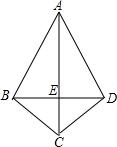如图，△ABC与△ADC关于直线AC对称，连接BD，若已知四边形ABCD的面积是125，AC=25，则BD的长为
如图，已知四边形ABCD的对角线互相垂直，若适当添加一个条件，就能判定该四边形是菱形．那么这个条件可以是（ ）
如图，已知四边形ABCD的四个顶点的坐标分别为A（0，0），B（9，0），C（7，5），D（2，7），将该四边形各顶点的横坐标都增加2，纵坐标都增加3，其面积为（ ）