题目内容
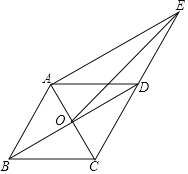
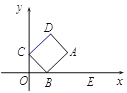
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 边上从点
边上从点![]() 运动到点
运动到点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,连
,连![]() ,在点
,在点![]() 运动过程中,请探究以下问题:
运动过程中,请探究以下问题:

(1)![]() 的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
(2)若![]() 为等腰三角形,求此时正方形
为等腰三角形,求此时正方形![]() 的边长.
的边长.
【答案】(1)不变,![]() ;(2)正方形ADEF的边长为
;(2)正方形ADEF的边长为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)作![]() 交
交![]() 延长线于
延长线于![]() ,证明
,证明![]() ,从而可得
,从而可得 ![]() ,继而根据三角形面积公式进行计算即可;
,继而根据三角形面积公式进行计算即可;
(2)分![]() 、
、![]() 、
、![]() 三种情况分别讨论求解即可.
三种情况分别讨论求解即可.
(1)作![]() 交
交![]() 延长线于
延长线于![]() ,
,
∵正方形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵矩形![]() 中,
中,![]() ,
,![]()
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ;
;

(2)①当![]() 时,作
时,作![]() ,
,
∵正方形![]() 中,
中,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
同(1)可得![]() ≌
≌![]() ,
,
∴![]() , ∴
, ∴![]() ,
,
∴![]() ;
;

②当![]() 时,
时,![]() ,
,
∵正方形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∵矩形![]() 中,
中,![]() ,
,
∴ ![]() ;
;

③当![]() 时,作
时,作![]() ,
,
同理得![]() ,
, ![]() ,
,
∴![]() ;
;

综上,正方形ADEF的边长为![]() 或
或![]() 或
或![]() .
.

【题目】为了从甲、乙两名学生中选择一人参加电脑知识竞赛,在相同条件下对他们的电脑知识进行了10次测验,成绩如下:(单位:分)
甲成绩 | 76 | 84 | 90 | 84 | 81 | 87 | 88 | 81 | 85 | 84 |
乙成绩 | 82 | 86 | 87 | 90 | 79 | 81 | 93 | 90 | 74 | 78 |
(1)请完成下表:
| 平均数 | 中位数 | 众数 | 方差 | 85分以上的频率 |
甲 | 84 | 84 | 14.4 | 0.3 | |
乙 | 84 | 84 | 34 |
(2)利用以上信息,请从三个不同的角度对甲、乙两名同学的成绩进行分析.
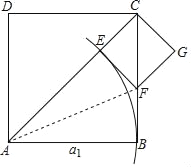
【题目】阅读下面材料:
已知:如图,在正方形ABCD中,边AB=a1.
按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关系,并且一个比一个小.
操作步骤 | 作法 | 由操作步骤推断(仅选取部分结论) |
第一步 | 在第一个正方形ABCD的对角线AC上截取AE=a1,再作EF⊥AC于点E,EF与边BC交于点F,记CE=a2 | (i)△EAF≌△BAF(判定依据是①); (ii)△CEF是等腰直角三角形; (iii)用含a1的式子表示a2为②: |
第二步 | 以CE为边构造第二个正方形CEFG; | |
第三步 | 在第二个正方形的对角线CF上截取FH=a2,再作IH⊥CF于点H,IH与边CE交于点I,记CH=a3: | (iv)用只含a1的式子表示a3为③: |
第四步 | 以CH为边构造第三个正方形CHIJ | |
这个过程可以不断进行下去.若第n个正方形的边长为an,用只含a1的式子表示an为④ | ||
请解决以下问题:
(1)完成表格中的填空:
① ;② ;③ ;④ ;
(2)根据以上第三步、第四步的作法画出第三个正方形CHIJ(不要求尺规作图).
【题目】2019年4月23日世界读书日这天,某校初三年级的小记者,就2018年寒假读课外书数量(单位:本)做了调查,他们随机调查了甲、乙两个班的10名同学,调查过程如下,请补充完整.
收集数据甲、乙两班被调查者读课外书数量(单位:本)统计如下:
甲:1,9,7,4,2,3,3,2,7,2
乙:2,6,6,3,1,6,5,2,5,4
整理、描述数据绘制统计表如下,请补全下表:
班级 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 4 | ______ | 3 | 5.6 |
乙 | 4 | 6 | ______ | 3.2 |
分析数据、推断结论
(1)该校初三乙班共有40名同学,你估计2018年寒假读6本书的同学大概有______人;
(2)你认为甲、乙两班同学寒假读书情况更好的是_______,理由是:______.