题目内容
 如图,平面直角坐标系中,点A(0,4),B(3,0),D、E在x轴上,F为平面上一点,且EF⊥x轴,直线DF与直线AB互相垂直,垂足为H,△AOB≌△DEF,设BD=h.
如图,平面直角坐标系中,点A(0,4),B(3,0),D、E在x轴上,F为平面上一点,且EF⊥x轴,直线DF与直线AB互相垂直,垂足为H,△AOB≌△DEF,设BD=h.
(1)若F坐标(7,3),则h=______,若F坐标(-10,-3),则DH=______;
(2)如h= ,则相对应的F点存在______个,并请求出恰好在抛物线y=
,则相对应的F点存在______个,并请求出恰好在抛物线y= 上的点F的坐标;
上的点F的坐标;
(3)请求出4个值,满足以A、H、F、E为顶点的四边形是梯形.
解:∵A(0,4),B(3,0)
∴OA=4 OB=3
∵△AOB≌△DEF
∴DE=4 EF=3
(1)若F坐标(7,3),则 0E=7 EF=3 OD=7-4=3
∵OB=3
∴h=BD=0
若F坐标(-10,-3),如图,则OE=10 DE=4 OD=6
∴BD=OD+OB=9
∵△FED∽△BHD
∴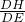 =
= 即
即 =
=
∴DH=

(2)若h= ,则点D坐标为D1(-
,则点D坐标为D1(- ,0)或D2(
,0)或D2(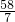 ,0),如图所示,相对应的F点共有4个.
,0),如图所示,相对应的F点共有4个.

∵OE1=-4- =-
=-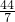 OE2=4-
OE2=4- =
= OE3=3+
OE3=3+ +4=
+4= OE4=3+
OE4=3+ -4=
-4=
∴这4个点的坐标分别是 F1(-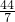 ,3 ) F2(
,3 ) F2( ,3)F3(
,3)F3( ,3 ) F4(
,3 ) F4( ,3)
,3)
分别把这4个点代入抛物线y= 中可得点 F2(
中可得点 F2( ,3)在抛物线上.
,3)在抛物线上.
(3)∵FH⊥AB EF⊥x轴
∴FH与EF不可能平行
①当AF∥EH时,如图

此时,BD=h,则BH= h BE=4-h
h BE=4-h
∵△ABO∽△GEB
∴BE:GE:BG=3:4:5
∴BG= GE=
GE=
∵AF∥HE
∴△GEH∽△GFA
∴ =
=
∴ =
=
化简得:3h2-25h+25=0
解得:h=
②当FH∥AE时,如图△DEF∽△EAB

∴ =
=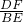
∵BE=BD-DE=h-4
∴ =
=
∴h=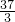
③当FH∥AE时,如图△DEF∽△EAB

∴ =
=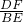
∵BE=BD+DE=h+4
∴ =
=
∴h=
综上可知:满足以A、H、F、E为顶点的四边形是梯形的h的4个值分别是 ,
, ,
,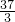 ,
, .
.
分析:(1)先根据题意求出DE=4,EF=3,确定点F的位置后可求出OB=3,所以h=BD=0;若F坐标(-10,-3),则OE=10,DE=4,OD=6,再根据△FED∽△BHD中的比例关系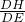 =
= 来求出DH=
来求出DH= .
.
(2)先根据h= ,求出点D坐标为(-
,求出点D坐标为(- ,0)或(
,0)或(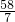 ,0)共两个,因为DH⊥AB,所以满足条件的DH有2条,每条DH上满足条件的F点有两个,所以共有4个.根据△AOB≌△DEF,DE=4,EF=3,可分别求出对应的4个F点的坐标,再分别代入抛物线y=
,0)共两个,因为DH⊥AB,所以满足条件的DH有2条,每条DH上满足条件的F点有两个,所以共有4个.根据△AOB≌△DEF,DE=4,EF=3,可分别求出对应的4个F点的坐标,再分别代入抛物线y= 中可确定在抛物线上的点F.
中可确定在抛物线上的点F.
(3)根据FH⊥AB,EF⊥x轴可以确定FH与EF不可能平行.所以从AF∥EH和FH∥AE两个方面进行分析.
当AF∥EH时BD=h,则BH= h BE=4-h,利用△ABO∽△GEB和△GEH∽△GFA得到
h BE=4-h,利用△ABO∽△GEB和△GEH∽△GFA得到 =
= ,代入对应的数值可得3h2-25h+25=0,从而求得h=
,代入对应的数值可得3h2-25h+25=0,从而求得h= .
.
当FH∥AE时,△DEF∽△EAB,此时分两种情况:一种是点F在第二象限,另一种是点F在第四象限.都可以用△DEF∽△EAB中的 =
=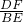 作为等量关系,得到关于h的方程,解方程即可求解.
作为等量关系,得到关于h的方程,解方程即可求解.
点评:本题的难点在第(3)题,要把握住梯形的性质,根据题意确定FH与EF不可能平行,从AF∥EH和FH∥AE两个方面进行分析是解题的关键.在有直角反复出现的图形中利用直角三角形的全等和相似来得到线段之间的数量关系是常用的方法.
∴OA=4 OB=3
∵△AOB≌△DEF
∴DE=4 EF=3
(1)若F坐标(7,3),则 0E=7 EF=3 OD=7-4=3
∵OB=3
∴h=BD=0
若F坐标(-10,-3),如图,则OE=10 DE=4 OD=6
∴BD=OD+OB=9
∵△FED∽△BHD
∴
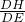 =
= 即
即 =
=
∴DH=


(2)若h=
 ,则点D坐标为D1(-
,则点D坐标为D1(- ,0)或D2(
,0)或D2(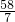 ,0),如图所示,相对应的F点共有4个.
,0),如图所示,相对应的F点共有4个.
∵OE1=-4-
 =-
=-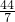 OE2=4-
OE2=4- =
= OE3=3+
OE3=3+ +4=
+4= OE4=3+
OE4=3+ -4=
-4=
∴这4个点的坐标分别是 F1(-
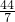 ,3 ) F2(
,3 ) F2( ,3)F3(
,3)F3( ,3 ) F4(
,3 ) F4( ,3)
,3)分别把这4个点代入抛物线y=
 中可得点 F2(
中可得点 F2( ,3)在抛物线上.
,3)在抛物线上.(3)∵FH⊥AB EF⊥x轴
∴FH与EF不可能平行
①当AF∥EH时,如图

此时,BD=h,则BH=
 h BE=4-h
h BE=4-h∵△ABO∽△GEB
∴BE:GE:BG=3:4:5
∴BG=
 GE=
GE=
∵AF∥HE
∴△GEH∽△GFA
∴
 =
=
∴
 =
=
化简得:3h2-25h+25=0
解得:h=

②当FH∥AE时,如图△DEF∽△EAB

∴
 =
=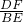
∵BE=BD-DE=h-4
∴
 =
=
∴h=
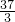
③当FH∥AE时,如图△DEF∽△EAB

∴
 =
=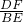
∵BE=BD+DE=h+4
∴
 =
=
∴h=

综上可知:满足以A、H、F、E为顶点的四边形是梯形的h的4个值分别是
 ,
, ,
,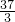 ,
, .
.分析:(1)先根据题意求出DE=4,EF=3,确定点F的位置后可求出OB=3,所以h=BD=0;若F坐标(-10,-3),则OE=10,DE=4,OD=6,再根据△FED∽△BHD中的比例关系
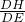 =
= 来求出DH=
来求出DH= .
.(2)先根据h=
 ,求出点D坐标为(-
,求出点D坐标为(- ,0)或(
,0)或(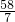 ,0)共两个,因为DH⊥AB,所以满足条件的DH有2条,每条DH上满足条件的F点有两个,所以共有4个.根据△AOB≌△DEF,DE=4,EF=3,可分别求出对应的4个F点的坐标,再分别代入抛物线y=
,0)共两个,因为DH⊥AB,所以满足条件的DH有2条,每条DH上满足条件的F点有两个,所以共有4个.根据△AOB≌△DEF,DE=4,EF=3,可分别求出对应的4个F点的坐标,再分别代入抛物线y= 中可确定在抛物线上的点F.
中可确定在抛物线上的点F.(3)根据FH⊥AB,EF⊥x轴可以确定FH与EF不可能平行.所以从AF∥EH和FH∥AE两个方面进行分析.
当AF∥EH时BD=h,则BH=
 h BE=4-h,利用△ABO∽△GEB和△GEH∽△GFA得到
h BE=4-h,利用△ABO∽△GEB和△GEH∽△GFA得到 =
= ,代入对应的数值可得3h2-25h+25=0,从而求得h=
,代入对应的数值可得3h2-25h+25=0,从而求得h= .
.当FH∥AE时,△DEF∽△EAB,此时分两种情况:一种是点F在第二象限,另一种是点F在第四象限.都可以用△DEF∽△EAB中的
 =
=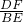 作为等量关系,得到关于h的方程,解方程即可求解.
作为等量关系,得到关于h的方程,解方程即可求解.点评:本题的难点在第(3)题,要把握住梯形的性质,根据题意确定FH与EF不可能平行,从AF∥EH和FH∥AE两个方面进行分析是解题的关键.在有直角反复出现的图形中利用直角三角形的全等和相似来得到线段之间的数量关系是常用的方法.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.