Question

【题目】阅读理解材料一：一组对边平行，另一组对边不平行的四边形叫梯形，其中平行的两边叫梯形的底边，不平行的两边叫梯形的底边，不平行的两边叫梯形的腰，连接梯形两腰中点的线段叫梯形的中位线．梯形的中位线具有以下性质：梯形的中位线平行于两底和，并且等于两底和的一半．

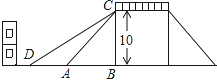
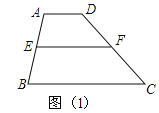
如图（1）：在梯形ABCD中：AD∥BC，

∵E、F是AB、CD的中点，∴EF∥AD∥BC，EF=（AD+BC）

材料二：经过三角形一边的中点与另一边平行的直线必平分第三边

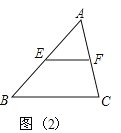
如图（2）：在△ABC中：∵E是AB的中点，EF∥BC

∴F是AC的中点

请你运用所学知识，结合上述材料，解答下列问题．

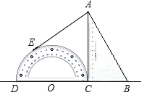
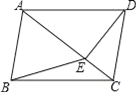
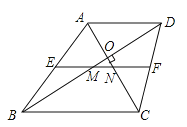
如图（3）在梯形ABCD中，AD∥BC，AC⊥BD于O，E、F分别为AB、CD的中点，∠DBC=30°．

（1）求证：EF=AC；

（2）若OD=，OC=5，求MN的长．

Answer 1

【答案】（1）证明见试题解析；（2）2．

【解析】

（1）由直角三角形中30°的锐角所对的直角边是斜边的一半，可得OA=AD，OC=BC，即可证明；

（2）直角三角形中30°的锐角所对的直角边是斜边的一半，得出OA=3，利用平行线得出ON=MN，再根据AN=AC=4，得出ON=4﹣3=1，进而得出MN的值．

解：（1）∵AD∥BC，∴∠ADO=∠DBC=30°，∴在Rt△AOD和Rt△BOC中，OA=AD，OC=BC，∴AC=OA+OC=（AD+BC），∵EF=（AD+BC），∴AC=EF；

（2）∵AD∥BC，∴∠ADO=∠DBC=30°，∴在Rt△AOD和Rt△BOC中，OA=AD，OC=BC，∵OD=，OC=5，∴OA=3，∵AD∥EF，∴∠ADO=∠OMN=30°，∴ON=MN，∵AN=AC=（OA+OC）=4，∴ON=AN﹣OA=4﹣3=1，∴MN=2ON=2．